流形间的点映射
\(\phi\)
,可以看作对点的推前映射
\(\phi=\phi_*\)
;对张量(场)
\(T\)
的拉回映射
\(\phi^*\)
,可看成该张量(场)
\(T\)
与某种推前映射
\(\phi_*\)
的复合映射
\(\phi^*T=T\circ\phi_*\)
;对张量(场)
\(T\)
的推前映射
\(\phi_*\)
,可看成该张量(场)
\(T\)
与某种拉回映射
\(\phi^*\)
的复合映射
\(\phi_*T=T\circ\phi^*\)
。
...
曲率概念的意义
导数算符对易子
\([\nabla_a,\nabla_b]=\nabla_a\nabla_b-\nabla_b\nabla_a\)
:对标量场的作用结果为0(无挠性决定的),但对一般张量场未必为0。
黎曼曲率张量就是这种非对易性的表现。
...
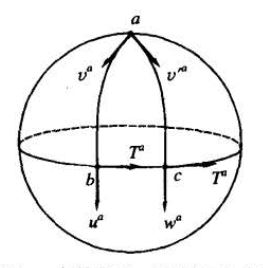
平移是路径无关的吗?
我们知道,欧氏空间的平移是路径无关的,任意两个位置,平移的结果是唯一的。
那么在流形上呢?结论是:流形上的平移是路径依赖的。只需要一个例子就足以说明,如图:
...
定义
导数算符,就是欧氏空间我们所熟悉的
\(\vec\nabla\)
,作用于标量场
\(f\)
就是梯度
\(\vec\nabla f\)
,作用于矢量场
\(\vec v\)
再缩并就是散度
\(\vec\nabla \cdot \vec v\)
。欧氏空间是有度规的,我们知道在有度规的情况下,度规可对张量指标进行“上升下降操作”,所以任何矢量都存在其自然对应的对偶矢量。如果要推广到任意流形,就必须分清楚矢量和对偶矢量(因为没有度规了)。
...
简介
抽象指标记号(英语:abstract index notation)是由罗杰·彭罗斯发明的一种用来表示张量与旋量的数学记号。与不带指标的字母(如T)表示张量相比,这种表示法能够显示张量的类型,同时可清楚地表明缩并等运算。而与用分量(张量在某一特定基底下的分量)表示张量不同,该表示法与特定的基底无关,可以表示出张量等式。
...