微分几何中的计算（Julia版 计划长期维护）

2020-02-24

| 微分几何 | | 流形 , julia , 张量 , 克氏符 , 黎曼曲率 , killing | 评论

Julia，对数学符号真太友好了。

前面的笔记中，我曾穿插了些相关的符号计算，本文作为一个汇总，并且未来的一些有特点的代码，我也将汇总于此，用作备忘。

用Julia进行张量符号计算的关键：1）先要写出（多重）数组友好的公式，然后用Julia实现之； 2）使用了SymPy，外加Julia本身的语法优势。

我曾想过将代码封装成函数，但发现直接用代码似乎更好。首先代码不复杂，其次， 暴露代码细节还能和数学公式相互对照，不容易出错。 有种“所见即所得”的感觉。

流形上的平移

2020-01-17

| 微分几何 | | 流形 , 平移 , 方向导数 , 联络 , 导数算符 , 克氏符 , 测地线 | 评论

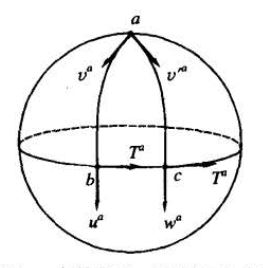
平移是路径无关的吗？

我们知道，欧氏空间的平移是路径无关的，任意两个位置，平移的结果是唯一的。

那么在流形上呢？结论是：流形上的平移是路径依赖的。只需要一个例子就足以说明，如图：

流形上的导数算符

2020-01-15

| 微分几何 | | 流形 , 导数算符 , 克氏符 | 评论

定义

导数算符，就是欧氏空间我们所熟悉的 \(\vec\nabla\) ，作用于标量场 \(f\) 就是梯度 \(\vec\nabla f\) ，作用于矢量场 \(\vec v\) 再缩并就是散度 \(\vec\nabla \cdot \vec v\) 。欧氏空间是有度规的，我们知道在有度规的情况下，度规可对张量指标进行“上升下降操作”，所以任何矢量都存在其自然对应的对偶矢量。如果要推广到任意流形，就必须分清楚矢量和对偶矢量（因为没有度规了）。