流形上的平移
平移是路径无关的吗?
我们知道,欧氏空间的平移是路径无关的,任意两个位置,平移的结果是唯一的。
那么在流形上呢?结论是:流形上的平移是路径依赖的。只需要一个例子就足以说明,如图:
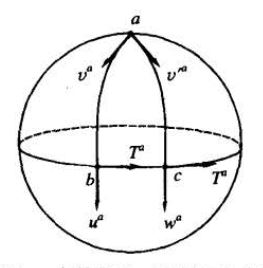
我们选择b为起点a为终点,路径1: \(b\to c\to a, u^a\to w^a \to v'^a\) ,路径2: \(b\to a, u^a\to v^a\) 。很明显不一样的路径,平移后的结果不一样。
所以,我们只能谈论沿曲线的平移。
矢量场沿曲线的平移
1. 平移概念
所谓平移,就是矢量移动后不变,所谓沿线平移,就是矢量
\(v^a\)
沿曲线
\(C(t)\)
移动后不变,所谓不变,数学含义就是(对欧氏空间而言):
\[
\frac{d v^a}{d t}=0
\]
而曲线
\(C(t)\)
的切矢是
\(T^a\overset{\Delta}{=}\left(\dfrac{d}{d t}\right)^a=\dfrac{d x^\mu}{dt}\left(\dfrac{\partial}{\partial x^\mu}\right)^a=T^\mu\left(\dfrac{\partial}{\partial x^\mu}\right)^a\)
,于是我们可以推导:
由此可见,对欧氏空间而言,
\(T^b\partial_b v^a\)
可解释成矢量场
\(v^a\)
沿曲线
\(C(t)\)
的导数,或沿
\(T^b\)
的导数。 这就是欧氏空间中的方向导数。
对一般流形而言,平移概念很自然推广成:设
\(v^a\)
是沿曲线
\(C(t)\)
的矢量场,
\(v^a\)
称为沿
\(C(t)\)
平移的,若
\(\dfrac{D v^a}{dt}\overset{\Delta}{=}T^b\nabla_b v^a=0\)
。其中
\(\dfrac{D v^a}{dt}\)
用来表示流形中沿曲线的方向导数。
2. 方向导数导数在局域坐标中的表达式
如果引入局域坐标系 \(\{x^\mu\}\) ,利用导数算符的结论和张量展式,可将 \(T^b\nabla_b v^a\) 表示为: \[ T^b\nabla_b v^a=\left(\frac{\partial}{\partial x^\mu}\right)^a\left[\frac{d v^\mu}{dt}+\Gamma^\mu_{\ \ \upsilon\sigma}T^\upsilon v^\sigma\right] \]
3. 沿曲线平移矢量场的唯一性
根据一阶常微分方程给定初值的解的唯一性,我们有结论:
曲线上一点 \(C(t_0)\) 及该点的一个矢量决定一个唯一的沿曲线平移的矢量场.
4. 联络
对流形中的任何两个点
\(p,q\)
,一般而言,
\(V_p,V_q\)
是两个不同的矢量空间,他们的元素是无法比较的。现在由于有了导数算符
\(\nabla_a\)
,于是可用一条曲线
\(C(t)\)
连接两点
\(p,q\)
,又由沿曲线平移矢量的唯一性,我们可以在
\(V_p,V_q\)
间定义一个映射
\(\varphi\)
:
\[
\begin{aligned} \varphi&:&V_p&\to V_q \\ & & v^a &\mapsto v^a 沿曲线 C(t) 平移到 q 点 \end{aligned}
\]
通过这个映射
\(\varphi\)
(曲线依赖的),原来毫无联系的
\(V_p,V_q\)
发生了某种联系,因此也把
\(\nabla_a\)
称为联络。
与度规适配的导数算符
在流形
\(M\)
上有导数算符(或联络)
\(\nabla_a\)
可以谈平移,如果还指定了度规
\(g_{ab}\)
就可以谈内积了。为了和欧氏空间的平移一致,谈平移还需要补充一个条件:平移时内积不变:
\[
0=\frac{d}{dt}(g_{ab}u^a v^b)=T^c \nabla_c(g_{ab}u^a v^b)=u^a v^b T^c \nabla_c g_{ab}
\]
由于这个条件对任意曲线和沿它平移的任意两个矢量
\(u^a,v^b\)
都成立,于是有:
\[
\nabla_c g_{ab}=0
\]
我们称满足这个条件的导数算符
\(\nabla_a\)
是度规适配的导数算符。
现在任意选择一个导数算符 \(\tilde{\nabla}_a\) (不要求度规适配),有: \[ 0=\nabla_a g_{bc}=\tilde{\nabla}_a g_{bc}-C^d_{\ \ ab} g_{dc}-C^d_{\ \ ac} g_{bd}=\tilde{\nabla}_a g_{bc}-C_{cab}-C_{bac} \] 即: \[ \tilde{\nabla}_a g_{bc}=C_{cab}+C_{bac} \] 轮换指标得另外两式: \[ \tilde{\nabla}_b g_{ca}=C_{abc}+C_{cba} \\ \tilde{\nabla}_c g_{ab}=C_{bca}+C_{acb} \]
第1式+第2式-第3式,再利用 \(C_{cab}=C_{cba}\) 得:
\[ \tilde{\nabla}_a g_{bc}+\tilde{\nabla}_b g_{ac}-\tilde{\nabla}_c g_{ab}=2 C_{cab} \]最后有:
\[
C^c_{\ \ ab}=\frac{1}{2}g^{cd}[\tilde{\nabla}_a g_{bd}+\tilde{\nabla}_b g_{ad}-\tilde{\nabla}_d g_{ab}]
\]
根据这个式子,我们可以认定:度规适配的导数算符是唯一的。否则必然存在另一个不同的度规适配的导数算符
\(\tilde{\nabla}_a\)
也满足
\(\tilde{\nabla}_c g_{ab}=0\)
,代入上式会导致
\(C^c_{\ \ ab}=0\)
,这说明
\(\nabla_a=\tilde{\nabla}_a\)
,矛盾。
由于度规适配导数算符的唯一性,以后有度规时,我们谈导数算符都默认是指度规适配的。
有度规流形中的克氏符
在流形 \((M,g_{ab})\) 上,有唯一的适配导数算符 \(\nabla_a\) ,选择一个局域坐标系 \(\{x^\mu\}\) ,根据上一小段的结论,克氏符克写成: \[ \Gamma^c_{\ \ ab}=\frac{1}{2}g^{cd}[\partial_a g_{bd}+\partial_b g_{ad}-\partial_d g_{ab}] \] 进而克氏符克分量可写成: \[ \Gamma^\sigma_{\ \ \mu \upsilon}=\frac{1}{2}g^{\sigma \rho}[g_{\upsilon \rho,\mu}+g_{\mu \rho,\upsilon}-g_{\mu \upsilon,\rho}] \]
测地线
在
\((M,\nabla_a)\)
中,有了矢量平移的概念,就很容易定义测地线: 就是满足切矢沿线平移的特殊曲线。
如果有度规场,那么
\((M,g_{ab})\)
的测地线是指
\((M,\nabla_a)\)
上的测地线,其中
\(\nabla_a\)
是与
\(g_{ab}\)
适配的。
利用前面的结论可很容易写出测地线方程:
\[
\frac{d^2 x^\mu}{dt^2}+\Gamma^\mu_{\ \ \upsilon\sigma}\frac{d x^\upsilon}{dt} \frac{d x^\sigma}{dt} = 0, \quad \mu=1,\dots
\]