基于抽象指标的张量分析

2020-01-14

| 微分几何 | | 流形 , 抽象指标 , 张量 , 对称性 , 坐标变换 , julia | 评论

简介

抽象指标记号（英语：abstract index notation）是由罗杰·彭罗斯发明的一种用来表示张量与旋量的数学记号。与不带指标的字母（如T）表示张量相比，这种表示法能够显示张量的类型，同时可清楚地表明缩并等运算。而与用分量（张量在某一特定基底下的分量）表示张量不同，该表示法与特定的基底无关，可以表示出张量等式。

抽象指标的直观意义(通过比较自己感受)

在纯矢量分析中，我们已经很自然用了 \(\vec{v}\) 这个抽象指标的原型，但为何到高阶张量反而不用？　在不用抽象指标的情况下，我只能复用 \(T^\mu_{\ \ \upsilon}\) ，它即表示张量，也表示张量分量，　更严格或许会指着 \(T\) 说，这是一个 \((1,1)\) 型张量。　如果引入了抽象指标，不但形式上能和 \(\vec{v}\) 一致，而且同 \(\vec{v}\) 一样，是坐标无关的。

抽象指标的要点

1. 用拉丁字母 \(a,b,c,\dots\) 作为上下标的抽象指标。比如，矢量 \(\vec v\) 可写成 \(v^a\) ，注意 \(a\) 在这里仅仅代表这个矢量箭头，不代表 \(1,2,3,\dots\) 。　类似地，对偶矢量可表示成 \(\omega_a\) 。 进而， (2,1)型张量可写成 \(T^{ab}_{\ \ \ c}\) 。　
2. 由于是抽象指标， \(\upsilon^a\) 和 \(\upsilon^b\) 独立而言代表相同的矢量，但如果在一个等式中必须注意指标平衡。 比如： \(\alpha u^a+v^a=w^a\) 和 \(\alpha u^b+v^b=w^b\) 代表同一个等式，但写成 \(\alpha u^a+v^b=w^a\) 就不对了。也就是说等号两边不但张量型必须一致，抽象指标也必须一致。
3. 具体指标用小写希腊字母 \(\mu,\upsilon,\alpha,\beta,\dots\) 表示，对具体指标（比如 \(\mu\) ）而言，是可取 \(\mu=1,2,\dots\) 的。
4. 重复上下抽象指标表示对这两个指标求缩并。比如： \(T^a_{\ \ a}=T(e^{\mu*};e_\mu)=T^\mu_{\ \ \mu},T^{ab}_{\ \ \ a}=T(e^{\mu*},\bullet;e_\mu),T^{ab}_{\ \ \ b}=T(\bullet,e^{\mu*};e_\mu)\) 。
5. 在抽象指标体系中，张量积记号可以省略。比如：对(2,1)型张量 \(T\) 和(1,1)型张量 \(S\) ，张量积 \(T \otimes S\) 可写成 \(T^{ab}_{\ \ \ c}S^d_e\) 。
6. 一般而言， \(\omega \otimes \mu \neq \mu \otimes \omega\) ，这是因为两边同时作用于 \((v,u)\) 的结果一般是不等的： \(\omega \otimes \mu(v,u)=\omega(v) \mu(u)\ne\mu(v) \omega(u)=\mu \otimes \omega(v,u)\) 。这个不可交换性，改成抽象指标可表示成： \(\omega_a \mu_b \ne \mu_a \omega_b\) 。 但是另一方面，由于重复抽象指标代表缩并，那么 \(\omega \otimes\mu(v,u)\) 即可写成 \(\omega_a \mu_b v^a u^b\) ,也可写成 \(\mu_b \omega_a v^a u^b\) （都代表 \(\omega(v)\mu(u)\) ），所以 \(\omega_a \mu_b = \mu_b \omega_a\) 。这意味着张量的字母带着自己的抽象指标是可交换的。
7. 抽象指标可用具体指标表示： \(T^{ab}_{\ \ \ c}=T^{\mu\upsilon}_{\ \ \ \sigma}(e_\mu)^a(e_\upsilon)^b(e^\sigma)_c\) 其中 \((e_\mu)^a\) 代表第 \(\mu\) 个基矢， \((e^\sigma)_c\) 代表第 \(\sigma\) 个对偶基矢。注意：这个表达式本质是把 \(T=T^{\mu\upsilon}_{\ \ \ \sigma}e_\mu \otimes e_\upsilon \otimes e^{\sigma *}\) ，改写成的抽象指标形式。
8. 具体指标当然也可用抽象指标表示： \(T^{\mu\upsilon}_{\ \ \ \sigma}=T^{ab}_{\ \ \ c}(e^\mu)_a(e^\upsilon)_b(e_\sigma)^c\) 。
9. 在抽象指标观点下， \(T^{ab}_{\ \ \ c}\) 代表一个张量，而 \(T^{\mu\upsilon}_{\ \ \ \sigma}\) 仅仅代表一个数（分量）。
10. 可从线性映射的角度看待张量。比如： \(V\) 上(1,1)型张量 \(T^a_{\ \ b}\) ，既可以看成 \(V\) 到 \(V\) 的线性映射，也可以看成 \(V^*\) 到 \(V^*\) 的线性映射。因为 \(\forall v^b\in V,T^a_{\ \ b}v^b \in V\) ，同时也有 \(\forall \omega_a\in V^*,T^a_{\ \ b}\omega_a \in V^*\) 。 特别地， \(\delta^a_{\ \ b}\) 即表示从 \(V\) 到 \(V\) 的恒等映射，也表示从 \(V^*\) 到 \(V^*\) 的恒等映射。
11. 度规张量是一个(0,2)型对称张量，通常记做 \(g_{ab}\) 。很明显，可以看成是从 \(V\) 到 \(V^*\) 的一个线性映射。由于度规的特殊性，这个线性映射同时是同构映射，所以可将 \(v^b\) 和 \(g_{ab}v^b\) 进行同构意义上的认同，于是用相同符号表示： \(v_a=g_{ab}v^b\) 。同样的原因， \(g\) 的逆映射 \(g^{-1}\) 必然存在，用抽象指标表示成： \(g^{ab}\overset{\Delta}{=}(g^{-1})^{ab}\) 。采用类似的思路，也有 \(\omega^a=g^{ab}\omega_b\) 。 由此可见，度规张量 \(g_{ab}\) 及其逆 \(g^{ab}\) 可对任意张量进行指标的“下降”和“上升”。由于度规张量的可逆性，我们还有： \(g^{ab}g_{bc}=g^a_{\ \ c}=\delta^a_{\ \ c}\) 。最后，不难证明，在具体指标下，也有类似的性质。
12. 由于涉及度规时，存在“升降指标”的问题，所以建议上下两排指标错开。

张量的对称性

对张量 \(T_{ab}\) 而言，如果 \(T_{ab}=T_{ba}\) ，则称之为对称张量。如果 \(T_{ab}=-T_{ba}\) ，则称之为反对称张量。

张量 \(T_{ab}\) 的对称部分 \(T_{(ab)}\) 和反对称部分 \(T_{[ab]}\) 分别定义为： \[ \boxed{T_{(ab)}:=\frac{1}{2}(T_{ab}+T_{ba}),\quad T_{[ab]}:=\frac{1}{2}(T_{ab}-T_{ba})} \] 一般而言， \((0,l)\) 型张量 \(T_{a_1,\dots,a_l}\) 的对称和反对称部分定义为： \[ \boxed{\begin{aligned}T_{(a_1,\dots,a_l)}:=\frac{1}{l!}\sum_{\pi}{T_{a_{\pi(1)}},\dots,T_{a_{\pi(l)}}}\\ \quad \\ T_{[a_1,\dots,a_l]}:=\frac{1}{l!}\sum_{\pi}{\delta_{\pi} T_{a_{\pi(1)}},\dots,T_{a_{\pi(l)}}}\end{aligned}} \]

其中 \(\pi\) 代表 \((1,\dots,l)\) 的一种排列， \(\pi(i)\) 表示 \(\pi\) 排列中的第 \(i\) 个数字， \(\delta_{\pi}=\pm 1\) （偶排列取＋，奇排列取-）。

如果 \(T_{a_1,\dots,a_l}=T_{(a_1,\dots,a_l)}\) ，则称 \(T_{a_1,\dots,a_l}\) 为全对称的；如果 \(T_{a_1,\dots,a_l}=T_{[a_1,\dots,a_l]}\) ，则称 \(T_{a_1,\dots,a_l}\) 全反称的。

以上的内容也完全适用于 \((k,0)\) 型张量。

基本性质

全对称张量 \(T_{a_1,\dots,a_l}\) ，满足 \(\forall \pi,T_{a_1,\dots,a_l}=T_{a_{\pi(1)},\dots,a_{\pi(l)}}\) 。

全反称张量 \(T_{a_1,\dots,a_l}\) ，满足 \(\forall \pi,T_{a_1,\dots,a_l}=\delta_{\pi}T_{a_{\pi(1)},\dots,a_{\pi(l)}}\) 。

对 \((k,0)\) 型(上指标)全对称和全反称张量也有类似结论 。

缩并时括号具有“传染性”，以方括号为例（圆括号依然）： \[ \boxed{T_{[a_1,\dots,a_l]}S^{a_1,\dots,a_l}=T_{[a_1,\dots,a_l]}S^{[a_1,\dots,a_l]}=T_{a_1,\dots,a_l}S^{[a_1,\dots,a_l]}} \]

括号内同种子括号可以随意增删，比如： \[ \boxed{T_{[[ab]c]}=T_{[abc]}} \] 括号内加异种子括号得０，比如： \[ \boxed{T_{[(ab)c]}=0,\quad T_{([ab]c)}=0} \] 异种括号缩并得０，比如： \[ \boxed{T^{(abc)}S_{[abc]}=0} \] 全对称张量的反称部分为０，反之亦然： \[ \boxed{\begin{aligned}T_{a_1,\dots,a_l}=T_{(a_1,\dots,a_l)} \Rightarrow T_{[a_1,\dots,a_l]}=0\\ \quad \\ T_{a_1,\dots,a_l}=T_{[a_1,\dots,a_l]} \Rightarrow T_{(a_1,\dots,a_l)}=0\end{aligned}} \]

张量分量的坐标变换

作为用抽象指标表示的张量是绝对的，不依赖坐标系的。但对具体指标所表示的坐标分量是坐标系依赖的。特别地，如果我们选择坐标基矢 \((\frac{\partial }{\partial x^\mu})^a\) 和对偶坐标基矢 \((dx^\upsilon)_b\) 来充当 \((e_\mu)^a\) 和 \((e^\upsilon)_b\) , 张量分量可表示成：

当然我们也能选择一组新的坐标基矢，那么对应新的张量分量： \[ T'^{\mu\upsilon}_{\ \ \ \sigma}=T^{ab}_{\ \ \ c}(dx'^\mu)_a(dx'^\upsilon)_b(\frac{\partial }{\partial x'^\sigma})^c \] 新的坐标系和旧的坐标系之间的关系： \(x'^\mu=x'(x^1,\dots,x^d)\) ，据此容易可写其微分关系： \[ dx'^\mu=\frac{\partial x'^\mu}{\partial x^\upsilon}dx^\upsilon,\quad \frac{\partial }{\partial x'^\sigma}=\frac{\partial x^\upsilon}{\partial x'^\sigma}\frac{\partial }{\partial x^\upsilon} \] 代的 \(T'^{\mu\upsilon}_{\ \ \ \sigma}\) 表达式，整理并利用 \(T^{\mu\upsilon}_{\ \ \ \sigma}\) 的表达式，最后得到张量分量的表达式： \[ \boxed{T'^{\mu\upsilon}_{\ \ \ \sigma}=\frac{\partial x'^\mu}{\partial x^\alpha}\frac{\partial x'^\upsilon}{\partial x^\beta}\frac{\partial x^\gamma}{\partial x'^\sigma}T^{\alpha\beta}_{\ \ \ \gamma}} \] 虽然上面针对的是 \((2,1)\) 型张量及其分量，但对任意型张量都成立。只要注意：1)指标平衡，2)相同指标缩并，3)新旧坐标跟随指标而平衡，我们就能随时写下任意型张量分量的坐标变换。

范例

4维闵氏度规 \(\eta_{ab}\) 的抽象指标表示： \[ \eta_{ab}=\eta_{\mu \upsilon}(dx^\mu)_a(dx^\upsilon)_b \] 其中 \(\{(dx^\mu)_a\}\) 是洛伦兹坐标系的对偶基底。以 \(\{t,x,y,z\}\) 代表 \(\{x^0,x^1,x^2,x^3\}\) 。因为非０的 \(\eta_{\mu \upsilon}\) 只有 \(\eta_{00}=-1,\eta_{11}=\eta_{22}=\eta_{33}=1\) ，进而有： \[ \eta_{ab}=-(dt)_a(dt)_b+(dx)_a(dx)_b+(dy)_a(dy)_b+(dz)_a(dz)_b \] 于线元表达式 \(ds^2=-dt^2+dx^2+dy^2+dz^3\) 相应。如果改用球坐标系 \(\{t,r,\theta,\varphi \}\) 代表新坐标 \(\{x'^0,x'^1,x'^2,x'^3\}\) ，则由 \[ x=r\sin\theta\cos\varphi,y=r\sin\theta\sin\varphi,z=r\cos\theta \] 张量分量的变换关系可写成： \[ \eta'_{\mu\upsilon}=\frac{dx^\alpha}{dx'^\mu}\frac{dx^\beta}{dx'^\upsilon}\eta_{\alpha\beta}=\frac{dx^\alpha}{dx'^\mu}\eta_{\alpha\beta}\frac{dx^\beta}{dx'^\upsilon} \] 改写成矩阵形式，在Julia进行符号推演得到球形坐标下的度规矩阵 \([\eta'_{\mu\upsilon}]\) ：

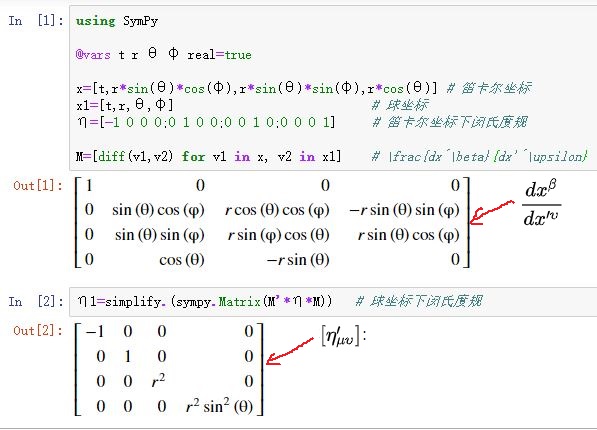
根据度规矩阵，容易写出度规张量： \[ \eta_{ab}=-(dt)_a(dt)_b+(dr)_a(dr)_b+r^2(d\theta )_a(d\theta )_b+r^2\sin^2\theta(d\varphi)_a(d\varphi)_b \] 对应的线元表达式就是： \[ ds^2=-dt^2+dr^2+r^2(d\theta^2+\sin^2\theta d\varphi^2) \]