流形上的旋量和旋量场(几何解释)
上一篇,引入旋量概念以及旋量代数。本篇在此基础上给出旋量的一个直观的几何解释。
本篇限定讨论闵氏时空上的旋量。
本篇的计算草稿:https://gitee.com/chaoskey/notes/blob/master/code/0077.ipynb
旋量的几何解释
一个旋量可以(如图)可解释成:(1)旗杆 “焊接” (2)旗 “加上” (3)旗与它周围事物之间的“指向-缠绕”关系。
当旗绕旗杆旋转 \(2\pi\) 时,旗可以完全复原【(1)+(2)两部分整体可复原】,但第(3)部分无法复原,旗杆需要再转 \(2\pi\) 才能使(3)复原。也就是说:旗绕旗杆旋转 \(2\pi\) 的任意奇数倍,旋量反向;旋转 \(2\pi\) 的任意偶数倍,旋量复原。
关于第(3)部分的理解,如下图(杯子(旗子)+环境(妹子)构成“指向-缠绕”):


零模矢量(旗杆)
给定一个旋量 \(\xi^A\in W\) ,我们可以构造一个作为“旗杆”的实零四维矢量 \(k^a\in V_p\) :
\[ k^a\to k^{AA'}=\xi^A\bar{\xi}^{A'} \]或写成分量形式【注意,上一篇中约定泡利矩阵前有因子 \(1/\sqrt{2}\) 】:
\[ k^\mu\sigma_\mu^{\ \ \Sigma\Sigma'}=\xi^\Sigma\bar{\xi}^{\Sigma'}\\ \quad \\ \frac{1}{\sqrt{2}}\begin{pmatrix} k^0+k^3 & k^1-ik^2 \\ k^1+ik^2 & k^0-k^3 \end{pmatrix} = \begin{pmatrix} \xi^1\bar{\xi}^{1'} & \xi^1\bar{\xi}^{2'} \\ \xi^2\bar{\xi}^{1'} & \xi^2\bar{\xi}^{2'} \end{pmatrix} \]右侧行列式为0,意味着 \(k^a\) 的确是零模矢量。此外,也可直接验证之:
\[ \begin{aligned}g_{AA'BB'}k^{AA'}k^{BB'}&=-(\epsilon_{AB}\xi^A\xi^B)(\bar{\epsilon}_{A'B'}\bar{\xi}^{A'}\bar{\xi}^{B'})\\ &=-(\xi_B\xi^B)(\bar{\xi}_{B'}\bar{\xi}^{B'})=-|\xi_B\xi^B|^2=0\end{aligned} \]因此可将 \(\xi^A\) 看成零模矢量 \(k^a\) 的“平方根”。
对任意两个旋量 \(\xi^A\) 和 \(\eta^A\) ,我们有:
\[ g_{AA'BB'}\xi^A\bar{\xi}^{A'}\eta^B\bar{\eta}^{B'}=-(\xi_B\eta^B)(\bar{\xi}_{B'}\bar{\eta}^{B'})=-|\xi_B\eta^B|^2 \]因此,任意旋量
\(\xi^A\)
和
\(\eta^A\)
所关联的零模矢量,都有一个非正内积(特指
\((-1,1,1,1)\)
对应的度规),这些零模矢量躺在光锥的同一半上(我们通常称之为未来光锥)。所以矢量空间
\(V_p\)
有一个自然的时间定向,可用一个实旋量张量表示这个定向:
\[
e_{AA'BB'CC'DD'}=i\left(\epsilon_{AB}\epsilon_{CD}\bar{\epsilon}_{A'C'}\bar{\epsilon}_{B'D'}-\bar{\epsilon}_{A'B'}\bar{\epsilon}_{C'D'}\epsilon_{AC}\epsilon_{BD}\right)
\]
容易验证:1) “实数性” 2)“全反称性” 【把
\(AA'\)
之类看成一个整体】。 进而对应
\(e_{abcd}=e_{[abcd]}\)
,这说明
\(e_{abcd}\)
的确是四维矢量空间
\(V_p\)
上的4形式,进而的确构成
\(V_p\)
上的定向。
如果 \(\eta^A\) 和 \(\xi^A\) 相差一个相位因子【旗因子】,比如, \(\eta^A=c\xi^A,\quad |c|=1,\quad c=e^{i\alpha}\) ,那么 \(\eta^A\) 和 \(\xi^A\) 关联着同一个零模矢量 \(k^a\) ,所以每个零模矢量都关联着一个单参旋量族。
二重矢量(旗)
为了进一步揭示“旗因子”的影响,转而研究由同一旋量 \(\xi^A\) 产生的实二重矢量 \(F^{ab}\) :
\[ F^{ab}\to F^{AA'BB'}=\xi^A\xi^B\bar{\epsilon}^{A'B'}+\bar{\xi}^{A'}\bar{\xi}^{B'}\epsilon^{AB} \]这个量只有不多余6个不同分量( \(F^{\mu\upsilon}=-F^{\upsilon\mu}\) )。
对给定非0旋量 \(\xi^A\) ,总能找到另一个旋量 \(\eta^a\) ,满足:
\[ \xi_A\eta^A=1 \]很明显, \(\{\xi^A,\eta^A\}\) 构成一组基旋量,进而:
\[ \epsilon^{AB}=\xi^A\eta^B-\eta^A\xi^B \]于是有:
\[ \begin{aligned}F^{AA'BB'}&=\xi^A\xi^B(\bar{\xi}^{A'}\bar{\eta}^{B'}-\bar{\eta}^{A'}\bar{\xi}^{B'})+\bar{\xi}^{A'}\bar{\xi}^{B'}(\xi^A\eta^B-\eta^A\xi^B)\\ &=\xi^A\bar{\xi}^{A'}(\xi^B\bar{\eta}^{B'}+\eta^B\bar{\xi}^{B'})-(\xi^A\bar{\eta}^{A'}+\eta^A\bar{\xi}^{A'})\xi^B\bar{\xi}^{B'}\\ &=\boxed{k^{AA'}l^{BB'}-l^{AA'}k^{BB'}}\end{aligned} \]其中:
\[ l^{AA'}\overset{\Delta}{=}\xi^A\bar{\eta}^{A'}+\eta^A\bar{\xi}^{A'} \]容易验证:
\[ \overline{l^{AA'}}=l^{AA'},\quad l^{AA'}l_{AA'}=-2,\quad k^{AA'}l_{AA'}=0 \]即【利用矢量的旋量表示】:
\[ \overline{l^{a}}=l^{a},\quad l^{a}l_{a}=2,\quad k^{a}l_{a}=0 \]这说明, \(l^a\) 是类空的,长度为 \(\sqrt{2}\) 的实四维矢量。并且和 \(k^a\) 正交。【在第一张图上也标记了对应的矢量】
在下面的变换下,
\[ \eta^A\to \eta^A+c\xi^A \]\(\{\xi^A,\eta^A\}\) 始终能构成同样好基旋量,同时有:【在第一张图上也标记了对应的矢量】
\[ l^a\to l^a+(c+\bar{c})k^a \]因此,由 \(\xi^A\) 构成的旋量张量 \(F^{AA'BB'}\) 代表着由两个四维矢量 \(k^a\) 和 \(l^a\) 构成的一个二重矢量 \(F^{ab}\) :
\[ F^{ab}=k^a l^b- l^a k^b \]“指向-缠绕”
考察旋量 \(\xi^A\) 乘上“旗因子” \(e^{i\alpha}\) 变换,则有:
\[ \xi^A_{\text{旋转}}=e^{i\alpha}\xi^A\quad \eta^A_{\text{旋转}}=e^{-i\alpha}\eta^A \]首先这个变换对矢量 \(k^a\) 没有影响,但对矢量 \(l^a\) 有影响(绕 \(k^a\) 旋转 \(2\alpha\) ):
\[ \begin{aligned}l^a_{\text{旋转}}\to l^{AA'}_{\text{旋转}}&=e^{2i\alpha}\xi^A\bar{\eta}^{A'}+e^{-2i\alpha}\eta^A\bar{\xi}^{A'}\\ &=\cos 2\alpha(\xi^A\bar{\eta}^{A'}+\eta^A\bar{\xi}^{A'})+\sin 2\alpha(i\xi^A\bar{\eta}^{A'}-i\eta^A\bar{\xi}^{A'})\\ &\to \boxed{l^a\cos 2\alpha+m^a\sin 2\alpha}\end{aligned} \]其中
\[ m^a\to m^{AA'}\overset{\Delta}{=}i(\xi^A\bar{\eta}^{A'}-\eta^A\bar{\xi}^{A'}) \]\(m^a\) 共享了矢量 \(l^a\) 的下述性质:1)实的;2)类空的;3)长度 \(\sqrt{2}\) ;4)与旗杆的零模四维矢量 \(k^a\) 正交;5)除相差 \(k^a\) 实倍数 \((c+\bar{c})\) 外,唯一由起初的旋量 \(\xi^A\) 确定。 此外, \(m^a\) 和 \(l^a\) 也是正交的。
因此, \(\{l^a,m^a\}\) 为某个二维空间提供基矢,“旗的尖端”就是在此二维空间中经历了旋转,并且旋转的角度是 \(2\alpha\) 。
旋量、旗杆和旗
如果我们将 \(k^a\) 这个零模四维矢量想象成从地球某点O照到月球某点P的激光,那么OP在三维空间的表示如图:
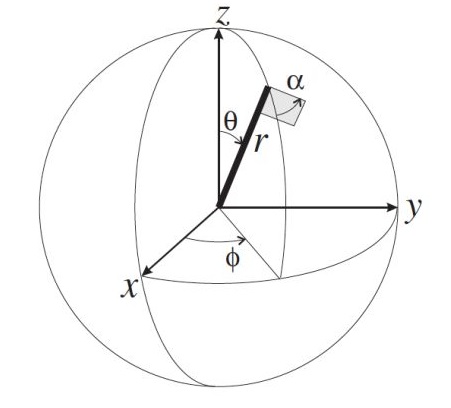
进而四维矢量 \(k^a\) 的分量可表示成:
\[ (k^\mu)=\begin{pmatrix} k^0 \\ k^1 \\ k^2 \\ k^3 \end{pmatrix}=\begin{pmatrix} r \\ r\sin \theta \cos \phi \\ r\sin \theta \sin \phi \\ r \cos \theta \end{pmatrix} \]根据旋量和矢量的关系,可解出对应旋量 \(\xi^A\) 的分量(精确到相差一个不确定“旗因子”):
\[ (\xi^\Sigma)=\begin{pmatrix} \xi^1 \\ \xi^2 \end{pmatrix}=\sqrt[4]{2}\sqrt{r}\begin{pmatrix} \cos\frac{\theta}{2}\ e^{-i(\phi-\alpha)/2} \\ \sin\frac{\theta}{2}\ e^{i(\phi+\alpha)/2} \end{pmatrix} \]旋量 \(\eta^A\) 可由 \(\xi^A\) 确定(精确到可加一个 \(\xi^A\) 的倍数):
\[ (\eta^\Sigma)=\begin{pmatrix} \eta^1 \\ \eta^2 \end{pmatrix}=\dfrac{1}{\sqrt[4]{2}\sqrt{r}}\begin{pmatrix} -\sin\frac{\theta}{2}\ e^{-i(\phi+\alpha)/2} \\ \cos\frac{\theta}{2}\ e^{i(\phi-\alpha)/2} \end{pmatrix} \]利用四维矢量 \(l^a\) 和旋量 \(l^{AA'}\) 的关系: \[ l^\mu\sigma_\mu^{\ \ AA'}= l^{AA'}=\xi^A\bar{\eta}^{A'}+\eta^A\bar{\xi}^{A'}\\ \text{改写成分量形式}\\ \frac{1}{\sqrt{2}}\begin{pmatrix} l^0+l^3 & l^1-il^2 \\ l^1+il^2 & l^0-l^3 \end{pmatrix} =\begin{pmatrix} \xi^1\bar{\eta}^{1'} & \xi^1\bar{\eta}^{2'} \\ \xi^2\bar{\eta}^{1'} & \xi^2\bar{\eta}^{2'} \end{pmatrix}+\begin{pmatrix} \eta^1\bar{\xi}^{1'} & \eta^1\bar{\xi}^{2'} \\ \eta^2\bar{\xi}^{1'} & \eta^2\bar{\xi}^{2'} \end{pmatrix} \]
将旋量分量表达式代入,并解出四维矢量 \(l^a\) 的所有分量:
\[ (l^\mu)=\begin{pmatrix} l^0 \\ l^1 \\ l^2 \\ l^3 \end{pmatrix}=\sqrt{2}\begin{pmatrix} 0 \\ \cos\theta\cos\phi\cos\alpha+\sin\phi\sin\alpha \\ \cos\theta\sin\phi\cos\alpha-\cos\phi\sin\alpha \\ -\sin \theta \cos \alpha \end{pmatrix} \]最后,不难算出二重矢量 \(F^{ab}\) (“旗”)的分量:
\[ F^{\mu\upsilon}=k^\mu l^\upsilon- l^\mu k^\upsilon \]