有限元法求解牛顿流体(FEniCS)
在Julia环境中,使用FenicsPy.jl调用
FEniCS库,求解偏微分方程。
纳维-斯托克斯方程组
纳维-斯托克斯方程:
\[ \color{red}{\frac{\partial \boldsymbol{u}}{\partial t}+(\boldsymbol{u} \cdot \nabla)\boldsymbol{u}=\frac{1}{\rho}\nabla\cdot \boldsymbol{\sigma}+\boldsymbol{f}} \]其中,张量
\(\boldsymbol{\sigma}\)
是应力张量, 取决于具体流体的特性假设,比如:牛顿流体。
连续性方程:
\[ \frac{\partial \rho}{\partial t}+\nabla \cdot (\rho \boldsymbol{u})=0 \]特别地,对不可压缩流体而言:
牛顿流体的特性假设:
\[ \color{blue}{\begin{aligned}\sigma(\boldsymbol{u},p) &= -p I + 2\mu \boldsymbol{\epsilon}(\boldsymbol{u}) \\ \boldsymbol{\epsilon}(\boldsymbol{u})&= \frac{1}{2}\left(\nabla \boldsymbol{u} + (\nabla \boldsymbol{u})^T \right)\end{aligned}} \]在 \(\color{blue}{牛顿流体假设}\) 下,这两个 \(\color{red}{红色方程}\) 的组成不可压缩牛顿流体的运动方程组。
对平面流体而言,这组方程有有三个方程,有三个待求量: 速度场 \(u(x,y,t)\) 和压强场 \(p(x,y,t)\) 。 给定边界条件,就可以求解了。
几个必要公式
\[ \begin{aligned}\boldsymbol{\epsilon}(\boldsymbol{u}) \cdot \nabla\boldsymbol{v}& =\epsilon_{ij}(\boldsymbol{u}) \frac{\partial v_i}{\partial x_j} \qquad \text{爱因斯坦求和约定} \\ &=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) \frac{\partial v_i}{\partial x_j} \\ &=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j} \frac{\partial v_i}{\partial x_j}+\frac{\partial u_i}{\partial x_j}\frac{\partial v_j}{\partial x_i}\right) \qquad \text{括号中第二项:由于缩并,指标交换不变} \\ &=\frac{\partial u_i}{\partial x_j}\frac{1}{2}\left(\frac{\partial v_i}{\partial x_j}+\frac{\partial v_j}{\partial x_i}\right) \\ &=\frac{1}{2}\left(\frac{\partial u_i}{\partial x_j}+\frac{\partial u_j}{\partial x_i}\right) \frac{1}{2}\left(\frac{\partial v_i}{\partial x_j}+\frac{\partial v_j}{\partial x_i}\right) \qquad \text{由于缩并,指标交换不变} \\ &=\boldsymbol{\epsilon}(\boldsymbol{u}) \cdot \boldsymbol{\epsilon}(\boldsymbol{v}) \qquad \text{这里的点乘,实际是双重指标缩并} \end{aligned} \]即(同时有第二式):
\[ \color{blue}{\boldsymbol{\epsilon}(\boldsymbol{u}) \cdot \nabla\boldsymbol{v} = \boldsymbol{\epsilon}(\boldsymbol{u}) \cdot \boldsymbol{\epsilon}(\boldsymbol{v}) = \nabla\boldsymbol{u} \cdot \boldsymbol{\epsilon}(\boldsymbol{v}) } \] \[ \color{blue}{\boldsymbol{\sigma}(\boldsymbol{u},p) \cdot \nabla\boldsymbol{v} = \boldsymbol{\sigma}(\boldsymbol{u},p) \cdot \boldsymbol{\epsilon}(\boldsymbol{v}) } \]不难根据“由于缩并,指标交换不变”类似推导出:
\[ \color{blue}{\boldsymbol{a} \cdot \left[\boldsymbol{\epsilon}(\boldsymbol{u}) \cdot \boldsymbol{v}\right] = \boldsymbol{a} \cdot \left[\nabla \boldsymbol{u} \cdot \boldsymbol{v}\right]} \]在此基础上,容易推导出:
\[ \color{red}{\left[\nabla \cdot \boldsymbol{\sigma}(\boldsymbol{u},p)\right]\cdot \boldsymbol{v} =2\mu\nabla \cdot \left[\nabla \boldsymbol{u} \cdot \boldsymbol{v}\right] -\nabla \cdot (p \boldsymbol{v}) - \boldsymbol{\sigma}(\boldsymbol{u},p) \cdot \boldsymbol{\epsilon}(\boldsymbol{v})} \]将运动方程转换成变分等式
利用前面的公式,将纳维-斯托克斯方程改写成变分等式(同时用了斯托克斯定理)
约定:
\[ \left<\boldsymbol{u},\boldsymbol{v}\right> \overset{\Delta}{=}\int_\Omega{\boldsymbol{u} \cdot \boldsymbol{v}d\omega}\qquad \left<\boldsymbol{u},\boldsymbol{v}\right>_{\partial \Omega} \overset{\Delta}{=}\int_{\partial \Omega}{\boldsymbol{u} \cdot \boldsymbol{v}ds} \]对时间有限差分 第1步:
已知 \(\boldsymbol{u}^n,p^n\) ,求 \(\color{red}{\boldsymbol{u}^*}\)
\[ \boxed{\begin{aligned}\rho\left<\frac{\boldsymbol{u}^*-\boldsymbol{u}^n}{\Delta t} , \boldsymbol{v}\right>+\rho\left<\boldsymbol{u}^n\cdot \nabla \boldsymbol{u}^n,\boldsymbol{v}\right>+\left<\boldsymbol{\sigma} ( \boldsymbol{u}^{n+\frac{1}{2}},p^n),\boldsymbol{\epsilon}(\boldsymbol{v})\right> \\ +\left< p^n \boldsymbol{n}, \boldsymbol{v} \right>_{\partial \Omega}-2\mu\left<\frac{\partial \boldsymbol{u}^{n+\frac{1}{2}}}{\partial n},\boldsymbol{v}\right>_{\partial \Omega}- \rho\left<\boldsymbol{f}^{n+1},\boldsymbol{v}\right>=0 \end{aligned}} \]其中:
\[ \frac{\partial \boldsymbol{u}}{\partial t} \approx \frac{\boldsymbol{u}^*-\boldsymbol{u}^n}{\Delta t} \qquad \boldsymbol{u}^{n+\frac{1}{2}} \approx \frac{\boldsymbol{u}^*+\boldsymbol{u}^n}{2} \]对时间有限差分 第2步:
已知 \(\boldsymbol{u}^*,p^n\) ,求 \(\color{red}{p^{n+1}}\) :
第1步对应得运动差分方程实际是:
\[ \frac{\boldsymbol{u}^*-\boldsymbol{u}^n}{\Delta t}+(\boldsymbol{u}^n \cdot \nabla)\boldsymbol{u}^n=\frac{1}{\rho}\nabla\cdot \boldsymbol{\sigma}(\boldsymbol{u}^{n+\frac{1}{2}}, p^n)+\boldsymbol{f}^n \]第2步需要运动差分方程则是:
\[ \frac{\boldsymbol{u}^{n+1}-\boldsymbol{u}^n}{\Delta t}+(\boldsymbol{u}^n \cdot \nabla)\boldsymbol{u}^n=\frac{1}{\rho}\nabla\cdot \boldsymbol{\sigma}(\boldsymbol{u}^{n+\frac{1}{2}},p^{n+1})+\boldsymbol{f}^n \]前后两式相减得:
\[ \frac{\boldsymbol{u}^*-\boldsymbol{u}^{n+1}}{\Delta t}=\frac{1}{\rho}\left(\nabla p^{n+1}-\nabla p^n\right) \]考虑到 \(\nabla \cdot \boldsymbol{u}^{n+1}=0\) ,对上式两边求散度后得:
\[ \frac{\nabla \cdot \boldsymbol{u}^*}{\Delta t}=\frac{1}{\rho}\left(\nabla^2 p^{n+1}-\nabla^2 p^n\right) \]根据这个等式可构建出变分等式:
\[ \boxed{\left<\nabla p^{n+1},\nabla q\right>=\left<\nabla p^n,\nabla q\right>-\frac{\rho}{\Delta t}\left<\nabla \cdot u^*, q\right>} \]对时间有限差分 第3步:
已知 \(\boldsymbol{u}^*,p^n,p^{n+1}\) ,求 \(\color{red}{\boldsymbol{u}^{n+1}}\) :
从第2步的公式:
\[ \frac{\boldsymbol{u}^*-\boldsymbol{u}^{n+1}}{\Delta t}=\frac{1}{\rho}\left(\nabla p^{n+1}-\nabla p^n\right) \]出发, 根据这个等式可构建出变分等式:
\[ \boxed{\left<\boldsymbol{u}^{n+1},\boldsymbol{v}\right>=\left<\boldsymbol{u}^*,\boldsymbol{v}\right>-\frac{\Delta t}{\rho}\left<\nabla\left(p^{n+1}-p^n\right),\boldsymbol{v}\right>} \]实现代码
前面方框中的公式,将在下面的代码中直接用到。
求解区域如图:

具体边界条件见有详细注释的代码。
# https://github.com/chaoskey/FenicsPy.jl
using FenicsPy
# 参数:ρ,μ,Δt
T = 5
num_steps = 5000
Δt = T / num_steps
μ = 0.001
ρ = 1
# 解域及网格生成
channel = Rectangle(Point(0.0, 0.0), Point(2.2, 0.41))
cylinder = Circle(Point(0.2, 0.2), 0.05)
Ω = channel - cylinder
mesh = generate_mesh(Ω, 64)
# 函数空间:速度场空间 和 压强场空间
V = VectorFunctionSpace(mesh, "P", 2)
Q = FunctionSpace(mesh, "P", 1)
# 定义边界: 入口,出口,墙,圆柱障碍
inflow = "near(x[0], 0)"
outflow = "near(x[0], 2.2)"
walls = "near(x[1], 0) || near(x[1], 0.41)"
cylinder = "on_boundary && x[0]>0.1 && x[0]<0.3 && x[1]>0.1 && x[1]<0.3"
# 入口边界的速度
inflow_profile = ("4.0*1.5*x[1]*(0.41 - x[1]) / pow(0.41, 2)", "0")
# 速度场边界条件
bcu_inflow = DirichletBC(V, Expression(inflow_profile, degree=2), inflow)
bcu_walls = DirichletBC(V, Constant((0, 0)), walls)
bcu_cylinder = DirichletBC(V, Constant((0, 0)), cylinder)
bcu = [bcu_inflow,bcu_walls,bcu_cylinder]
# 压力场边界条件
bcp_outflow = DirichletBC(Q, Constant(0), outflow)
bcp = [bcp_outflow]
# 下一时刻(待求)速度场u, 求解后保存在u_
u = TrialFunction(V)
u_ = FeFunction(V)
# 下一时刻(待求)压力场p, 求解后保存在p_
p = TrialFunction(Q)
p_ = FeFunction(Q)
# 速度场测试函数 和 压力场测试函数
v = TestFunction(V)
q = TestFunction(Q)
# 当前时刻(已知)速度场u 和 压力场p
u_n = FeFunction(V)
p_n = FeFunction(Q)
# (u^* + u^n)/2
# 注意:其中包含待求函数 u (即,u^*)
# 所以,包含U的变分方程F的a(u,v)必须用 lhs(F)求出
# 对应的L(v)则须用 rhs(F)求出
U = 0.5*(u_n + u)
# 法线
n = FacetNormal(mesh)
# 力场
f = Constant((0, 0))
# 在缩并的掩护下,可看作是对称梯度
function ϵ(u)
return sym(nabla_grad(u))
end
# 应力张量
function σ(u, p)
return 2*μ*ϵ(u) - p*Identity(len(u))
end
# 第1步的变分方程: (u^n,p^n) -> u^*
# 待求的u^*采用u, 结果计划保存在u_
F1 = ρ*dot((u - u_n) / Δt, v)*dx + ρ*dot(dot(u_n, nabla_grad(u_n)), v)*dx +
inner(σ(U, p_n), ϵ(v))*dx + dot(p_n*n, v)*ds -
dot(2*μ*nabla_grad(U)*n, v)*ds - ρ*dot(f, v)*dx
a1 = lhs(F1)
L1 = rhs(F1)
# 第2步的变分方程: (u^*,p^n) -> p^{n+1}
# u^* 采用第1步的结果 u_
# 待求的p^{n+1}采用p, 结果计划保存在p_
a2 = dot(nabla_grad(p), nabla_grad(q))*dx
L2 = dot(nabla_grad(p_n), nabla_grad(q))*dx - (ρ/Δt)*div(u_)*q*dx
# 第3步的变分方程: (u^*,p^n, p^{n+1}) -> u^{n+1}
# (u^*, p^{n+1}) 分别采用第1、2步的结果 (u_,p_)
# 待求的u^{n+1}采用u, 结果计划保存在u_
a3 = dot(u, v)*dx
L3 = dot(u_, v)*dx - (Δt/ρ)*dot(nabla_grad(p_ - p_n), v)*dx
# 三个变分方程对应的矩阵
A1 = assemble(a1)
A2 = assemble(a2)
A3 = assemble(a3)
# 将边界条件附加到矩阵上
[bc.apply(A1) for bc in bcu]
[bc.apply(A2) for bc in bcp]
# 创建XDMF文件(可视化)
xdmffile_u = XDMFFile("navier_stokes_cylinder/velocity.xdmf")
xdmffile_p = XDMFFile("navier_stokes_cylinder/pressure.xdmf")
# 创建时间序列
timeseries_u = TimeSeries("navier_stokes_cylinder/velocity_series")
timeseries_p = TimeSeries("navier_stokes_cylinder/pressure_series")
# 保存网格
File("navier_stokes_cylinder/cylinder.xml.gz") << mesh
global t = 0
for i in 1:num_steps
# 当前时间
global t += Δt
# 第一步
# lvsolve(a1,L1,u_,bcu) # 这个方法求解很慢
# 下面的方法更块的原因是,在循环前已经生成了变分方程对应的矩阵
b1 = assemble(L1)
[bc.apply(b1) for bc in bcu]
solve(A1, u_.vector(), b1, "bicgstab", "hypre_amg")
# 第二步
b2 = assemble(L2)
[bc.apply(b2) for bc in bcp]
solve(A2, p_.vector(), b2, "bicgstab", "hypre_amg")
# 第三步
b3 = assemble(L3)
solve(A3, u_.vector(), b3, "cg", "sor")
# 更新数据
u_n.assign(u_)
p_n.assign(p_)
if (i-1)%25 == 0 || i == num_steps
xdmffile_u.write(u_, t)
xdmffile_p.write(p_, t)
timeseries_u.store(u_.vector(), t)
timeseries_p.store(p_.vector(), t)
println("第",i,"步\t max:", max(array(u_)...))
# Plot solution
plot(u_)
plot(p_)
end
end
# 确保文件不被损坏
xdmffile_u.close()
xdmffile_p.close()
第0步 max:2.739542375402953
第25步 max:1.9848943489237132
第50步 max:1.917539036089884
… …
第4950步 max:2.178513430654289
第4975步 max:2.1431069545490455
第4999步 max:2.1574859438440463
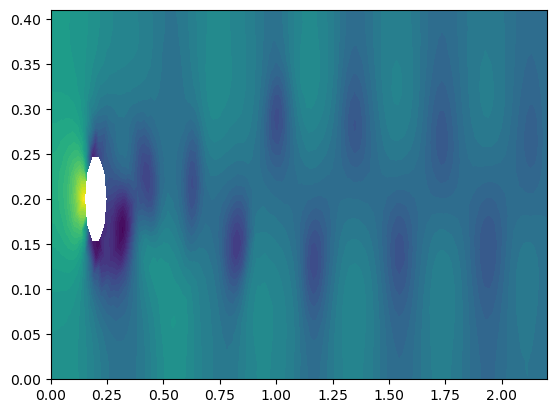
用ParaView渲染的结果如下(速度场 和 压力场):

