有限元法解偏微分方程(FEniCS)
在Julia环境中,使用FenicsPy.jl调用
FEniCS库,求解偏微分方程。
以泊松方程(第一边界条件)为例
\[ -\Delta u = f \qquad \boldsymbol{x} \in \Omega \\ u|_{\partial \Omega} =g \]范例而已, 本例提供的套路是通用的,大不了多看看文档。
关键的地方,我特意列出相关链接。
本文采用软件包: FEniCS。
第1步:将问题转化成变分等式
\[ \begin{aligned}a(u,v)&=L(v)+\int_{\partial \Omega}{\frac{\partial g}{\partial n}vds} \qquad \forall v \in \left\{v\in H^1(\Omega) \ : \ v|_{\partial \Omega} = g\right\} \\ a(u,v) &\overset{\Delta}{=} \int_\Omega{\nabla u \nabla v d\omega} \\ L(v) &\overset{\Delta}{=} \int_\Omega{f v d\omega} \end{aligned} \]因为第一边界条件可通过变换( \(u \to u + g\) )化归成0边值问题,所以只需要考虑对应的弱形式(0边界条件):
\[ a(u,v)=L(v) \qquad \forall v \in \left\{v\in H^1(\Omega) \ : \ v|_{\partial \Omega} = 0\right\} \]解出0边值问题后,不难通过简单变换得到非零边值问题的解。(这步,FEniCS会自动帮我们作了,不必操心)。
注意:第二、三边界条件就没那么简单了,对应的面积分项是不可省略的。
问题具体化为,比如:
\[ \begin{aligned} f(x,y)&=-6 \\ g(x,y)&=1+x^2+2y^2 \\ & \\ \Omega&=\left\{(x,y)|x^2+y^2 \le 1\right\} \end{aligned} \]特别说明:后续Julia代码涉及的变量名,完全和上面的公式一致。
第2步:对求解域进行刨分
这里用到了Circle, 更多请查阅文档:
https://bitbucket.org/fenics-project/mshr/wiki/API
也可以通过一组顶点组成的多边形来逼近更复杂的求解域,然后再对这个多边形区域进行刨分,更详细查阅文档:
这里的求解域很简单,代码如下:
# https://github.com/chaoskey/FenicsPy.jl
using FenicsPy
# 求解域Ω设定
Ω = Circle(Point(0.0, 0.0),1)
mesh = generate_mesh(Ω,16)
plot(mesh)
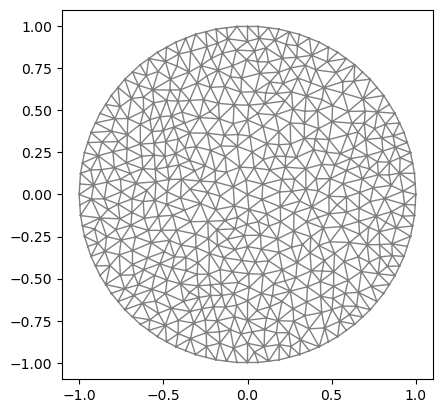
2-element Array{PyCall.PyObject,1}:
PyObject <matplotlib.lines.Line2D object at 0x7f8ddf8bd7d0>
PyObject <matplotlib.lines.Line2D object at 0x7f8ddf07d210>
第3步:构造基于网格的函数空间
函数空间(FunctionSpace),记作
\(V\)
,其定义为:
与此“孪生”对应:测试函数空间,记作
\(\hat{V}\)
:
这里我们的函数空间选择最简单的线性插值。
-
所谓
试探函数(TrialFunction), 特指 \(V\) 中的函数。 -
所谓
测试函数(testFunction), 则特指 \(\hat{V}\) 中的函数。
# 试探函数空间
# 1阶多项式插值(线性插值)
V = FunctionSpace(mesh, "P", 1)
# 函数空间V上的试探函数u
u = TrialFunction(V)
# 函数空间V上的测试函数v
v = TestFunction(V);
第4步:边界条件及参数设定
关于边界条件的设定参数,可参见:
https://fenicsproject.org/docs/dolfin/1.4.0/python/programmers-reference/cpp/fem/DirichletBC.html
# 源f(x,y)
# f = Expression('-6', degree=0)
f = Constant(-6.0)
# 边界值g(x,y)
g = Expression("1 + x[0]*x[0] + 2*x[1]*x[1]", degree=2)
bc = DirichletBC(V, g, "on_boundary");
第5步:变分方程的“直译”
几乎是前面数学公式的"直译", 需要注意的是: dx 是预定义量,代表体元, 对应公式中的
\(d\omega\)
。
# 定义变分问题(dx是预定的)
a = dot(grad(u), grad(v))*dx
L = f*v*dx;
第6步:求解并绘图
关于求解器solve,参见:
https://fenicsproject.org/docs/dolfin/1.3.0/python/programmers-reference/fem/solving/solve.html
但是在 FEniCS.jl中,分成了3个求解器(都是对fenics.solve的封装):
~~https://github.com/SciML/FEniCS.jl/blob/master/src/jsolve.jl~~
1. 线性求解器: solve
2. 线性变分求解器: lvsolve (本例所采用)
3. 非线性变分求解器: nlvsolve
由于FEniCS.jl不太好用,我重写了FEniCS的Julia封装:FenicsPy.jl。
至于FeFunction, 其实就是fenics.Function的封装(为了避免和类Core.Function和函数Base.Function的命名冲突)。
# 求解
u = FeFunction(V)
solve(a == L,u,bc)
plot(u)
plot(mesh)
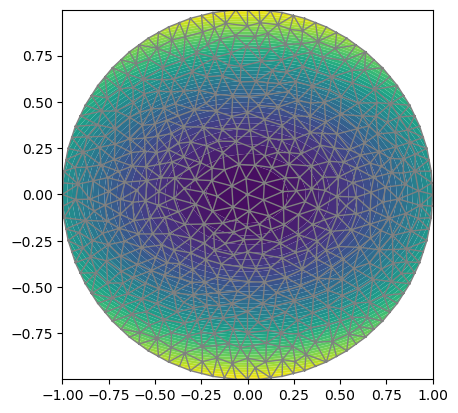
Solving linear variational problem.
2-element Array{PyCall.PyObject,1}:
PyObject <matplotlib.lines.Line2D object at 0x7f8dde997910>
PyObject <matplotlib.lines.Line2D object at 0x7f8dde997d10>
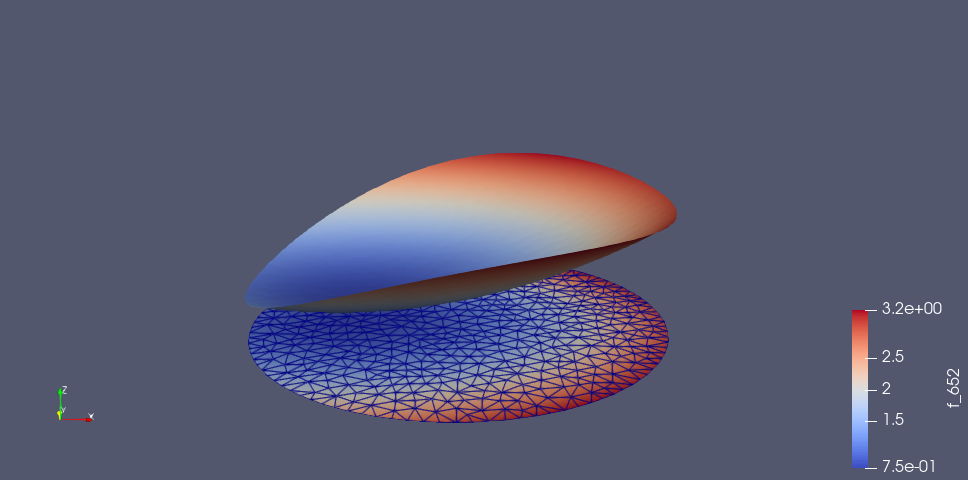
第7步:将数据导出,然后在ParaView中可视化
先用下面的代码导出数据为VTK文件。
然后在ParaView中打开,可以用交互的方式可视化(下图仅截图示意而已)
vtkfile = File("poisson/solution.pvd")
vtkfile << u; #exports the solution to a vtkfile

第8步:误差估计及其它
我们注意到,这个具体化的泊松问题的精确解,恰好就等于 \(g(x,y)=1+x^2+2y^2\) ,这种巧合源自:
\[ \Delta g(x,y) = 6 \]恰好把
\(f(x,y)=-6\)
提供的源抵消了,也就是说,如果作变换:
\(u = U + g(x,y)\)
,可得到无源零边界的泊松问题, 对应的解
\(U=0\)
,所以精确解就是:
\(u=g(x,y)\)
。
于是可以计算标准差:
\[ E = \sqrt{\int_\Omega{(g-u)^2}d\omega} \]可用函数errornorm计算之:
errornorm(g, u, "L2")
*** Warning: Degree of exact solution may be inadequate for accurate result in errornorm.
0.00444692071683997
也可以直接计算标准差(奇怪结果不一样,以后再细究):
#vertex_values_g = array(project(g, V))
# or
vertex_values_g = array(interpolate(g, V))
vertex_values_u = array(u)
sqrt(sum((vertex_values_g - vertex_values_u).^2))
0.0541946910486183
查看结果数据:
- 1)根据表达式生成在网格顶点上的值(投影)
# pg = project(g, V)
# or
pg = interpolate(g, V)
"Coefficient(FunctionSpace(Mesh(VectorElement(FiniteElement('Lagrange', triangle, 1), dim=2), 3), FiniteElement('Lagrange', triangle, 1)), 71)"
-
- 查看网格顶点上的值,比如:
array(pg)
array(u)
549-element Array{Float64,1}:
2.647985350348445
2.593690657292863
2.4339075463156465
2.712889645782536
2.3863642443300686
2.1981490620535595
2.1831070985479455
2.4655691189520748
2.7609431348948275
2.5253575052502386
2.302218396526692
2.4686047402353437
2.02311867450322
⋮
2.261621580085735
2.123167515460912
2.1160030006867037
2.2820357294253473
2.2320866025105017
2.176630600748635
2.0517861914831785
2.5936906572928624
2.5253575052502386
2.4686047402353433
2.4007647581013947
2.3454915028125263
初边值问题典型范例:热传导方程
\[ \left\{\begin{aligned}\frac{\partial u}{\partial t} &= \nabla^2 u + f & \mathrm{on} \quad \Omega \times (0,T] \\ u &= u_D & \mathrm{on}\quad \partial \Omega \times (0,T] \\ u &= u_0 & t=0 \end{aligned} \right . \]求解思路:对时间用差分法,对空间用有限元法。 进而有:
\[ \left\{\begin{aligned}a(u^{n+1},v) &= L_{n+1}(v) \qquad n\ge 1 , \quad v \in \left\{v \in H^1(\Omega) \ : \ v|_{\partial \Omega} = 0\right\} \\ a(u,v) &\overset{\Delta}{=} \int_{\Omega}{(u v + \Delta t\nabla u \cdot \nabla v)d\omega} \\ L_{n+1}(v) &\overset{\Delta}{=} \int_{\Omega}{(u^n + \Delta t f^{n+1})v d\omega} \\ u^0 &= u_0 \end{aligned} \right . \]具体化为, 比如:
\[ \begin{aligned} f(x,y,t)&=0 \\ u_D(x,y,t)&=0 \\ u_0(x,y)&=e^{-a(x^2+y^2)},\quad a=5 \\ & \\ \Omega&=[-2,2]\times[-2,2], \quad t \in [0,2] \end{aligned} \]T = 2.0 # 时长
num_steps = 50 # 步数
Δt = T / num_steps # 步长
# 在解域空间生成网格
nx = ny = 30
mesh = RectangleMesh(Point(-2, -2), Point(2, 2), nx, ny)
# 函数空间(线性插值)
V = FunctionSpace(mesh, "P", 1)
# 边界条件
bc = DirichletBC(V, Constant(0), "on_boundary")
# 初值
u_0 = Expression("exp(-a*pow(x[0], 2) - a*pow(x[1], 2))", degree=2, a=5)
u_n = interpolate(u_0, V)
# 定义变分问题
u = TrialFunction(V)
v = TestFunction(V)
f = Constant(0)
a = u*v*dx + Δt*dot(grad(u), grad(v))*dx
L = (u_n + Δt*f)*v*dx
# 创建VTK文件,用于保存解
vtkfile = File("heat_gaussian/solution.pvd")
# 从初值开始,逐步计算
u = FeFunction(V)
t = 0
for n in 1:num_steps
# 当前时间
global t += Δt
# 求解
solve(a == L,u,bc)
# 保存到文件,并叠加式绘图
vtkfile << (u, t)
plot(u)
# 更新上一时刻的解
u_n.assign(u)
end
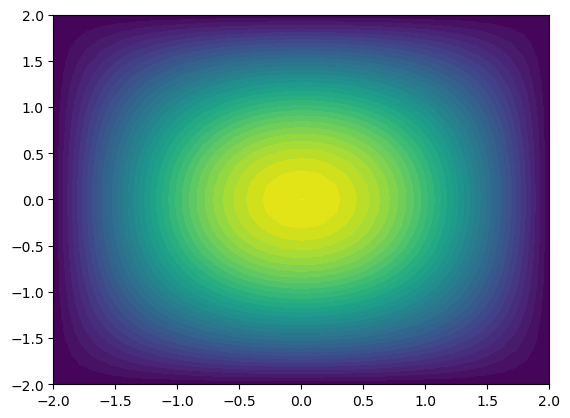
在ParaView中打开生成的VTK文件,进行适当可视化交互操作,然后录制成gif文件如下:

更复杂的边界条件(以泊松方程为例)
回到最开头的例子,但将泊松方程的边界条件修改为:
\[ \left\{\begin{aligned}-\Delta u &= f & \qquad \boldsymbol{x} \in \Omega \\ u &=u_L & \mathrm{on} \quad \partial \Omega_L \\ u &=u_R & \mathrm{on} \quad \partial \Omega_R \\ \frac{\partial u}{\partial n} &=g & \mathrm{on} \quad \partial\Omega \end{aligned}\right. \]此时,对应的变分方程应改为:
\[ \begin{aligned}a(u,v)&=L(v) \qquad \forall v \in \left\{v\in H^1(\Omega) \ : \ v|_{\partial \Omega} = 0\right\} \\ a(u,v) &\overset{\Delta}{=} \int_\Omega{\nabla u \nabla v d\omega} \\ L(v) &\overset{\Delta}{=} \int_\Omega{f v d\omega} +\int_{\partial \Omega}{g v ds} \end{aligned} \]问题具体化为(注意:提供的 \(u_L\) 和 \(u_R\) 必须保证其在边界上的连续性),比如:
\[ \begin{aligned} f(x,y)&=-6 \\ u_L(x,y)&=2+x+y^2 \\ u_R(x,y)&=3+x^2 \\ g(x,y)&=4y \\ & \\ \Omega&=\left\{(x,y)|x^2+y^2 \le 1\right\} \\ \partial\Omega_L&=\left\{(x,y)|x^2+y^2 = 1, x \le 0 \right\} \\ \partial\Omega_R&=\left\{(x,y)|x^2+y^2 = 1, x > 0 \right\} \end{aligned} \]在下面的Julia代码中, 前两个边界条件体现在DirichletBC的设置中,而第三个边界条件体现在变分方程中。
注意:正如预定义量dx代表体元,ds也是预定义量,代表面元。
# 求解域Ω设定
Ω = Circle(Point(0.0, 0.0),1)
mesh = generate_mesh(Ω,16)
# 函数空间(线性插值)
V = FunctionSpace(mesh, "P", 1)
u = TrialFunction(V)
v = TestFunction(V)
# 源f(x,y)
f = Constant(-6.0)
# 左右边界条件
u_L = Expression("2 + x[0] + pow(x[1], 2)", degree=2)
bc_L = DirichletBC(V, u_L, "on_boundary && x[0]<=0")
u_R = Expression("3 + pow(x[0], 2)", degree=2)
bc_R = DirichletBC(V, u_L, "on_boundary && x[0]>0")
# 诺伊曼边界条件
g = Expression("4*x[1]", degree=1)
# 定义变分问题(dx 和 ds 都是预定义的)
a = dot(grad(u), grad(v))*dx
L = f*v*dx + g*v*ds
# 求解
u = FeFunction(V)
solve(a == L,u,[bc_L,bc_R])
vtkfile = File("poisson2/solution.pvd")
vtkfile << u; #exports the solution to a vtkfile
plot(u)
plot(mesh)
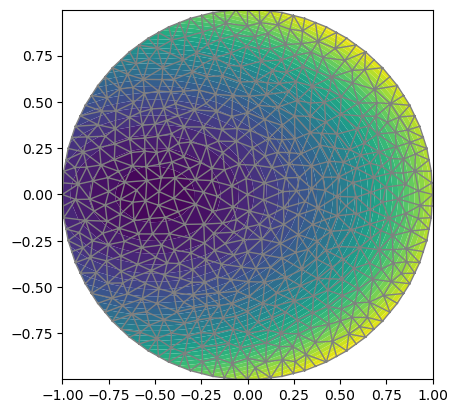
Solving linear variational problem.
2-element Array{PyCall.PyObject,1}:
PyObject <matplotlib.lines.Line2D object at 0x7f4af82ef6d0>
PyObject <matplotlib.lines.Line2D object at 0x7f4af82ef8d0>
在ParaView中打开生成的VTK文件,进行适当可视化交互操作,截图如下:
后记
本文着重有限元法的“套路”, 更多例子可参考:
https://fenicsproject.org/pub/tutorial/html/ftut1.html
至于,ParaView的用法,参考: