不可压缩流体的有限元【翻译】

2021-03-01

| 科学计算 | | FEniCS , 有限元法 , 偏微分方程 |

有限元方法的结构为用户提供了一个选择范围。对于解决不可压缩的流体问题尤其如此，因为理论上指出了许多稳定的有限元公式。我们使用自动化工具来实现和检查稳态Stokes方程的各种稳定公式。事实证明，FEniCS项目组件的表达能力使Stokes问题的求解器可以轻松创建使用各种单元公式。

20·1 Stokes方程

Stokes方程描述了稳定的不可压缩的低雷诺数流体。对于域 $\Omega\subset\mathbb{R}^d\quad 1\le d \le 3$ ，Stokes方程读着：

-\Delta u + \nabla p = f \qquad in\ \Omega \tag{20.1}

\nabla \cdot u = 0 \qquad in\ \Omega \tag{20.2}

u = 0 \qquad on\ \partial \Omega \tag{20.3}

其中， $u:\Omega \to \mathbb{R}^d$ 是速度场， $p:\Omega \to \mathbb{R}$ 是压力场， $f:\Omega \to \mathbb{R}^d$ 是源项。

在开发用于求解Stokes方程的变分公式时，可能是在无散度的函数空间中搜索（20.1）的变分公式的解，从而通过构造满足（20.2）。但是，这并不能很好地转换为有限元公式。或者，可以考虑一个混合变分公式如下。令 $V = [H_0^1(\Omega)]^d$ 和 $\Pi = \{q\in L^2(\Omega) : \int_{\Omega}q dx = 0\}$ 。给定 $f\in [L^2(\Omega)]^d$ ，寻求函数 $u\in V$ 和 $p\in\Pi$ ，满足：

a(u, v) − b(v, p) = ( f , v) \qquad \forall v \in V \tag{20.4}

b(u, q) = 0 \qquad \forall q \in \Pi \tag{20.5}

其中

a(u, v) := \int_{\Omega} \nabla u \cdot \nabla v dx \tag{20.6}

b(v, q) := \int_{\Omega}(\nabla \cdot v) q dx \tag{20.7}

( f , v) := \int_{\Omega} f \cdot v dx \tag{20.8}

20·2 混合Stokes问题的有限元公式

在本节中，我们将考虑寻求（20.4）-（20.5）混合公式的近似解所对应的有限元公式。在有限元方法的背景下，Stokes问题得到了广泛的研究，Brezzi和Fortin（1991）以及Brenner和Scott（2008）提出了一些关键结果。这在许多方面都是一个具有挑战性的问题。首先，必须仔细选择V和Π的有限元子空间，以确保所得有限元问题的稳定性。其次，混合变分形式是一个鞍点问题，这导致了不定矩阵方程。这样的系统在迭代线性求解器上特别费力。此外，质量守恒要求速度场无散度。很少有方案可以逐点满足此条件。施加此条件的程度取决于特定的方案。

用于Stokes方程的稳定的混合有限元方法必须满足Ladyzhenskaya–Babuška–Brezzi（LBB）（或inf–sup）的相容性条件（有关更多详细信息，请参阅Brezzi和Fortin（1991））。最直接的方案-压力和速度分量均等的连续拉格朗日有限元空间-导致不稳定的问题。此外，混合单元公式可以表现出“锁定”类型，在实践中有时可以通过对 $$b(v, q)$$ 型项使用不精确的正交来弥补（Engelman等，1982）。这已经被认为等同于改变压力空间。在这里，我们采用现代的观点，并使用已知满足LBB条件的速度和压力空间。

避免Stokes问题鞍点性质相关难题的方法是，通过用涉及压力的项来扩充连续性方程，以修正离散变分问题。通过适当解决离散问题，可以证明等阶公式的稳定性（Hughes等，1986）。仔细的修改会导致不会破坏一致性的离散问题。

很少有涉及多个有限元公式的关于Stokes问题的数值研究。这可以归因于许多难以实施的已知稳定方法。借助自动代码生成，可以轻松生成用于多种方法的求解器；它就像重新定义有限元素空间或修改变分公式一样简单。在本节的其余部分，我们将说明Stokes方程混合形式的各种稳定有限元求解器的构造。

20·2·1 基于兼容函数空间的公式

我们考虑了许多LBB稳定的公式，这些公式都是基于速度和压力场的兼容函数空间的选择。图20.1给出了大多数这些公式的通用UFL输入。按照UFL约定，双线性和线性形式分别命名为a和L。通过速度的单元类型（U_element），速度的基函数阶次（U_order），压力的单元类型（P_element）和压力的基函数阶次（P_order），定义出不同的有限元空间。从图20.1的输入中，FFC生成用于数值模拟的特定问题代码。

图20.1

图20.1 混合Stokes问题的通用UFL输入。

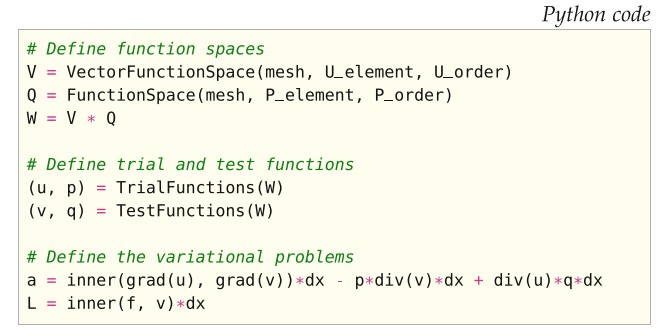
Stokes方程式中使用最广泛的有限元族之一是Taylor–Hood族（Taylor and Hood，1973; Boffi，1997）。它由用于速度分量的连续 $P_q (q \ge 2)$ 拉格朗日单元和用于压力场的连续 $P_{q−1}$ 拉格朗日单元组成（对于q = 3，请参见图20.2）。压力收敛的阶次低于速度的阶次。对于图20.1中的UFL提取，Taylor-Hood单元对应于P_element = Lagrange，U_order = q，P_element = Lagrange和P_order = q-1。

图20.2

图20.2 Taylor–Hood单元具有（a）三次速度基底和（b）二次压力基底。

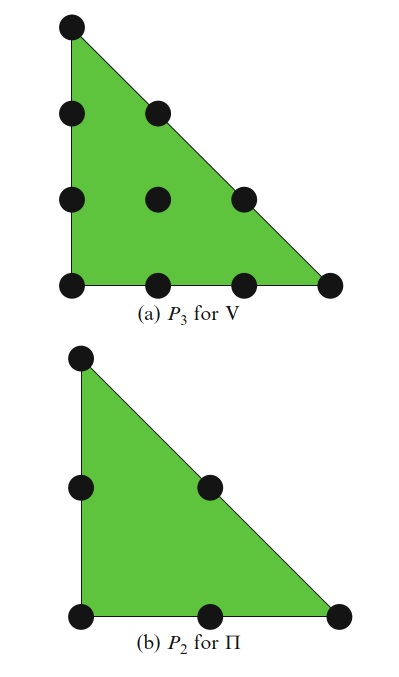
Crouzeix–Raviart单元（Crouzeix和Raviart，1973年）是一种不符合的单元，它使用胞元边上的积分矩作为速度的基底，并且不连续的压力空间要比速度空间低一个级次。对于最低阶情况，速度边矩等效于每个边中点的拉格朗日基函数的求值，压力使用 $$P_0$$ （见图20.3）。对于图20.1中的提取，Crouzeix–Raviart单元对应于U_element = CR，U_order = 1，P_element = DiscontinuousLagrange和P_order = 0。

图20.3

图20.3 Crouzeix–Raviart单元用于速度场。

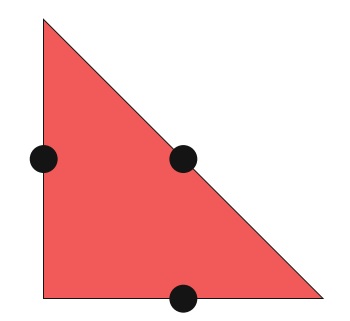
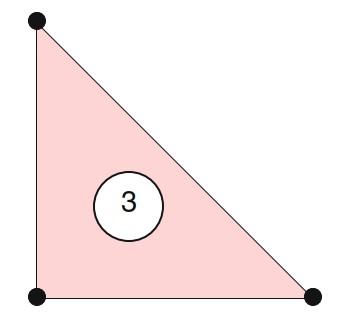
MINI单元（Arnold等，1984b）通过气泡函数 $P_q + B_{q + 3}$ 增强速度空间。 MINI单元如图20.4所示。压力空间使用连续的 $$P_q$$ 拉格朗日单元。有人建议将MINI单元替换为更廉价的Taylor-Hood单元。 MINI单元是使用来自UFL的“单元增强”概念来实现的。 MINI函数空间的UFL定义如图20.5所示。在写此内容时，仅适用于 $$q = 1, 2$$ 。

图20.4

图20.4 用于速度场的MINI单元。它使用

\(q + 3\)

阶气泡函数增强了

\(P_q\)

单元。

图20.5

图20.5 定义MINI元素速度空间的UFL输入。

另一种可能性是对速度分量使用高阶连续拉格朗日有限元基底，而对压力场使用的不连续单元则要低两阶。对于连续速度/不连续压力，我们将这个单元简称为“CD”。 Brezzi和Fortin（1991）讨论了P2-P0的情况，Maday等人（1992）则中分析了高阶版本。对于图20.1中的提取，CD单元对应于U_element = Lagrange，U_order = q，P_element = DiscontinuousLagrange和P_order = q-2。

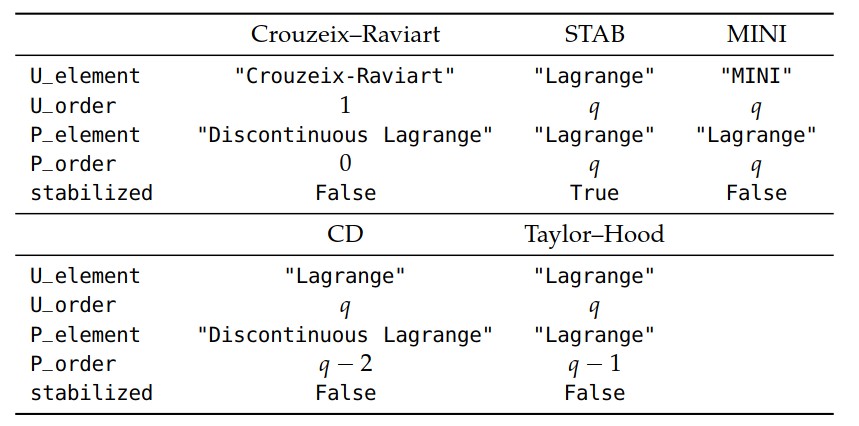
表20.1总结了图20.1所示UFL代码中针对所介绍的不同方法的特定变量。

表20.1

表20.1 定义不同混合方法的单元变量。

20·2·2 压力稳定法

为了减轻查找LBB兼容函数空间的困难，可以使用稳定化技术。压力稳定将有限维公式从鞍点问题转换为强制问题。通常希望修改有限维问题，以免破坏一致性。有关更完整的讨论，请参见Donea和Huerta（2003）。我们考虑的压力稳定方法涉及：

a(u, v) − b(v, p) = ( f , v)\qquad \forall v \in V_h \tag{20.9}

b(u, q) + (\delta \nabla q, \nabla p) = ( f , \delta \nabla q)\qquad \forall q \in \Pi_h \tag{20.10}

其中， $\delta$ 是一个稳定参数，而 $V_h\subset V$ 和 $\Pi_h \subset\Pi$ 是合适的有限元空间。对于我们的测试， $\delta= 0.2 h^2_T$ ，其中 $$h_T$$ 是胞元 $$T$$ 周长的两倍。对于稳定化测试，对压力和速度空间使用相同阶次的连续拉格朗日单元。该方法称为“ STAB”。我们采用的稳定方法很简单，但确实违反了阶次 $$q>1$$ 的一致性。图20.6说明了将稳定项添加到图20.1中的标准弱形式中。表20.1包含了STAB单元的定义。

图20.6

图20.6 UFL代码为图20.1中的混合方法代码增加了稳定性。

20·3 惩罚方法：Scott–Vogelius方法

处理LBB条件的其他解决方案包括Uzawa迭代方法和惩罚方法。这两种方法的结合导致了Scott和Vogelius（1985）中提出的迭代惩罚方法。令 $r\in\mathbb{R}$ 和 $\rho\in\mathbb{R}^{+}$ 为规定参数。我们希望寻求 $u_n\in V_h$ 以满足

a(u^n, v) + r(\nabla \cdot u^n, \nabla \cdot v) = ( f , v) − (\nabla \cdot v, \nabla \cdot w^n)\qquad \forall v \in V_h \tag{20.11}

其中

w^{n+1} = w^n + \rho u^n \tag{20.12}

可以通过 $p =\nabla\cdot w-C$ 用辅助场 $$w$$ 来表示压力，其中 $$C$$ 是任意常数（因为压力场只能确定相差任意一个常数）。在计算 $$p$$ 中的误差时，我们减去 $\nabla\cdot w$ 的平均值，以计入 $$C$$ 。该算法最初假定 $$w_0 = 0$$ ，然后求解（20.11）并通过（20.12）更新 $$w$$ 。重复该过程，直到 $\|u^{n + 1} -u^n\| <\epsilon$ ，其中 $\epsilon$ 是规定的公差。该方法仅涉及一个函数空间，但是它需要一个高阶连续单元（ $q\ge 4$ ），并且可以精确地解决无散度准则。迭代次数和精度取决于惩罚参数 $\rho$ 和 $$r$$ 。对于我们的实验，我们使用 $\rho= −r = 1\times 10^3$ 。此公式的实现如图20.7所示。

图20.7

图20.7 DOLFIN代码，用于定义Scott-Vogelius方法。

20·4 数值测试

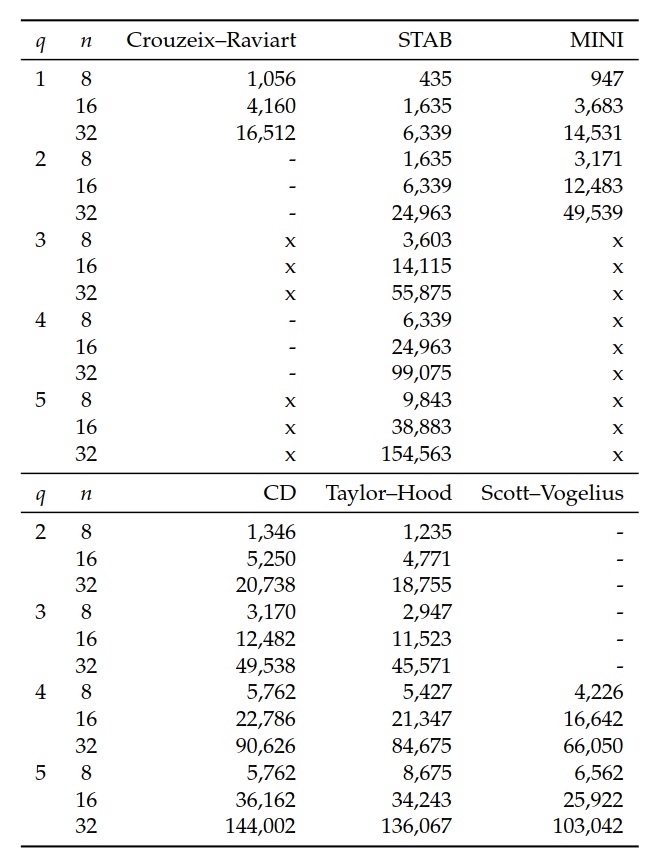
为了评估提出的方法，我们将计算结果与针对不同网格细化和单元阶次所制造的解进行比较。所有模拟都使用FEniCS工具通过UMFPACK LU求解器（来自SuiteSparse软件包v3.4）来生成离散问题（FFC v0.7.0，DOLFIN v0.9.4，UFL v0.4.0，UFC v1.2.0）。对于应用于Stokes问题的迭代方法，请参阅第35章和Elman等（2005）。表20.2给出了所考虑情况下自由度数与网格尺寸和单元类型的函数。

表20.2

表20.2 比较由速度阶数（q）和每个维度（n）的网格划分数组成的自由度数。 “-”表示该特定单元阶次不稳定； “ x”表示当前尚未实现。

20·4·1 模拟设置

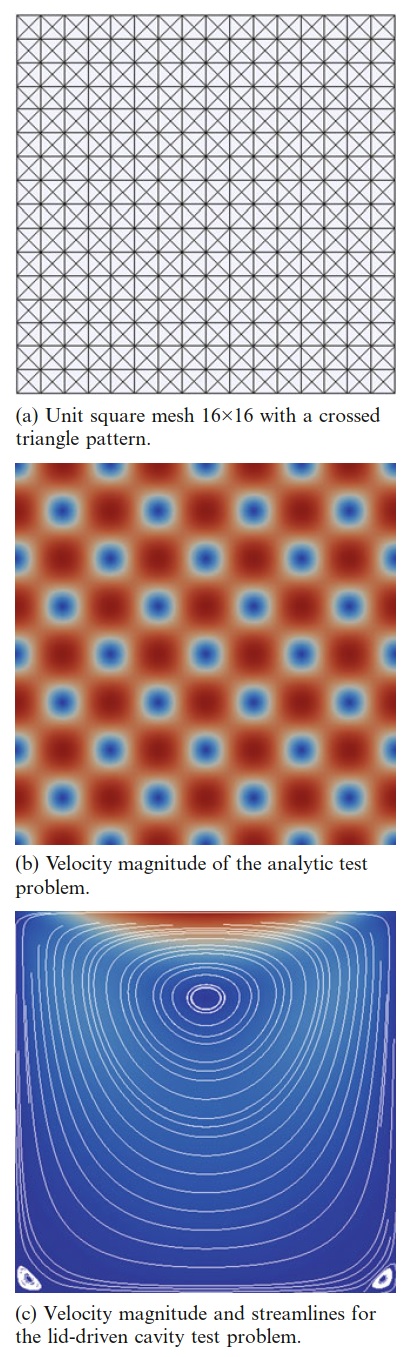
对于我们的测试，我们使用具有交叉三角形图案的n×n单位正方形网格，如图20.8a所示。应该注意的是，网格的选择可能会以令人惊讶的方式影响收敛结果，例如避免锁定现象（Nagtegaal等，1974）或杂散压力模式（Malkus，2000）。交叉的三角形网格用作我们的测试案例，以避免与网格构造有关的细微问题（请参阅Brezzi和Fortin（1991年，建议6.1，第VI.6节））。此外，由于我们从一开始就使用稳定单元，因此我们不关心锁定现象。为了进行比较，请在非交叉网格上使用带有杂散压力模式校正的网格，请参见Terrel等（2008）。

图20.8

图20.8 测试网格和解绘制。

作为第一个测试用例，我们使用以下Stokes方程的解析解：

f = \begin{bmatrix}−28\pi^2\sin(4\pi x) \cos(4\pi y) \\ -36\pi^2 \cos(4\pi x) \sin(4\pi y)\end{bmatrix} \tag{20.13}

u = \begin{bmatrix}−\sin(4\pi x) \cos(4\pi y) \\ \cos(4\pi x) \sin(4\pi y)\end{bmatrix} \tag{20.14}

p = \pi \cos(4\pi x) \cos(4\pi y) \tag{20.15}

我们还考虑了在顶部具有二次驱动功能的盖驱动腔问题（见图20.8b和20.8c）。

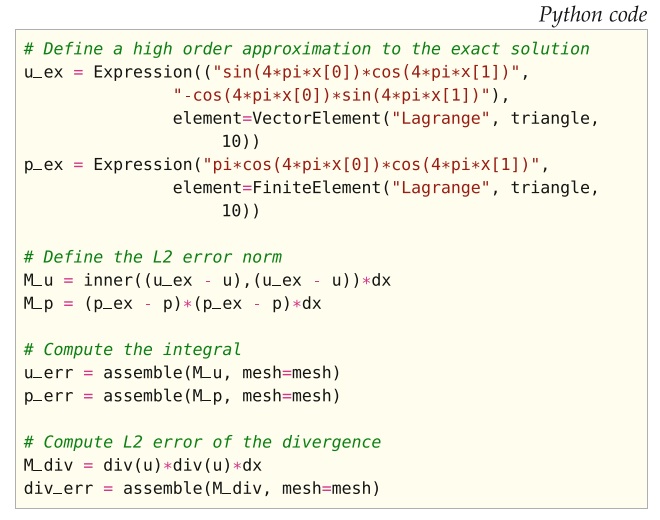
图20.9和20.10显示了所考虑的问题的DOLFIN Python代码。为了从分析测试问题变为盖驱动腔，只需要改变边界条件函数和右侧 $$f$$ 。只能由一个任意常数决定的压力场在一个压力自由度为零的情况下被“钉住”。给定网格和定义的变分问题之一，DOLFIN将使用FFC和FIAT自动生成必要的计算机代码，从而允许使用一个脚本来测试所有方法。在根据功能规范计算分析测试用例的误差时，使用10阶的拉格朗日单元来插值精确解。计算误差的代码如图20.11所示。

图20.9

图20.9 用于定义测试域的DOLFIN代码。

图20.10

图20.10 DOLFIN代码，用于定义盖驱动腔域。

图20.11

图20.11 DOLFIN代码，用于计算

\(L^2\)

范数中的误差。精确解使用胞元上的10阶拉格朗日多项式进行插值。

20·4·2 结果

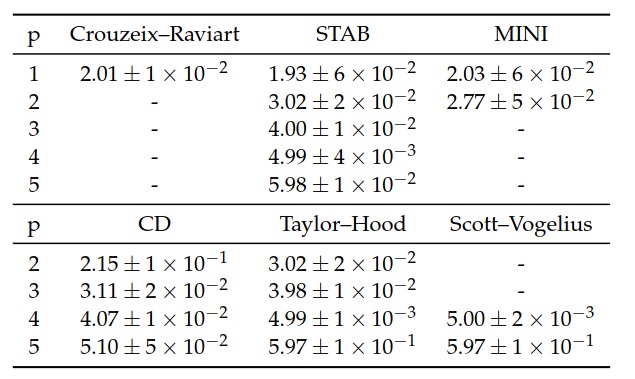
表20.3给出了在每种情况下，分析方法在速度场的L2范数中观测到的收敛速度，这是根据n在{8、16、32、64}中的一系列网格细化计算得出的。除CD单元外，所有公式均可观察到的最佳速率为q+1。由于差的压力近似和不能满足LBB条件，CD单元失去了一个收敛阶。

表20.3

表20.3 计算速度收敛速度的指数；就是，

\(q\)

在

\(O(h^q)\)

中，其中h是网格单元的宽度。对于不同的单元，此误差使用

\(L^2\)

，其中

\(q = p + 1\)

是最优误差率，其中p是速度场的阶次。请注意，如理论上所预期的，CD方法失去收敛阶数，而MINI单元在二阶情况下效果不佳。

要进一步比较的方法中，一些用于与适当选择的压力空间的四阶速度空间的情况下，给出了误差和性能度量。使用分析测试用例。 Crouzeix–Raviart和MINI单元仅适用于低阶基底。为了进行比较，它们是在一个细网格上计算的，该细网格的自由度与四阶Taylor–Hood单元具有相似的自由度。图20.12比较了不同方法的速度 $$L^2$$ 误差。对所有的单元，速度近似似乎都是收敛的。压力的 $$L^2$$ 误差如图20.13所示。对于CD单元，观察到压力的不可预测行为，而对于其他方法，观察到压力场的收敛。图20.14给出了速度场散度的 $$L^2$$ 范数。正如理论所预测的，对于所有网格，在机器精度以内，Crouzeix–Raviart和Scott–Vogelius方法的散度误差为零。 MINI单元的散度误差比其他方法大得多。图20.15给出了各种四阶情况的运行时间。使用2.6 GHz Intel Xeon，在所有运行时，都可以使用Python代码测量组装和线性系统求解时间。假定代码生成所需的时间可以忽略不计，因为生成的代码已缓存，并且仅影响第一次仿真的时间；我们的时间总是来自第二次仿真。混合单元的运行时间随自由度的数量而定。 Scott-Vogelius方法对于迭代求解器具有更好的性质，因此，尽管相对于测试小问题的其他方法而言，运行时间更长，但它对于大规模问题可能具有吸引力。

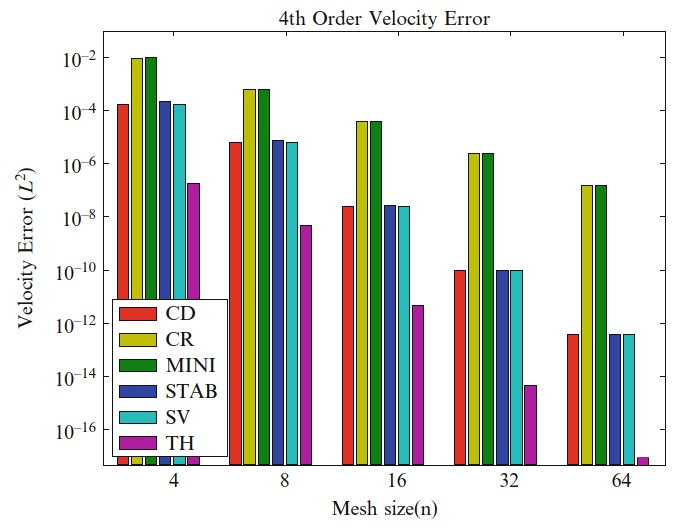
图20.12

图20.12 分析测试用例的速度误差。

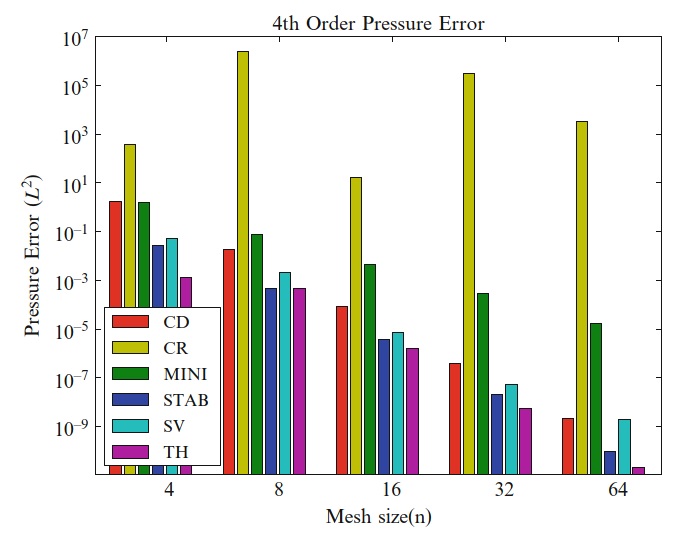
图20.13

图20.13 分析测试用例的压力误差。

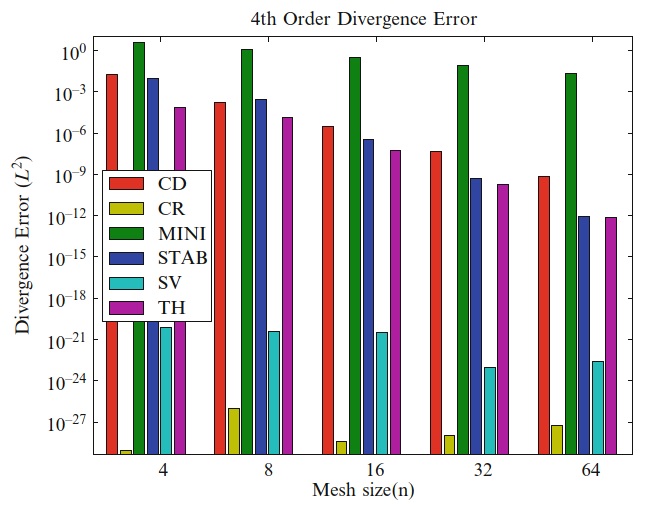
图20.14

图20.14 分析测试用例的散度误差。

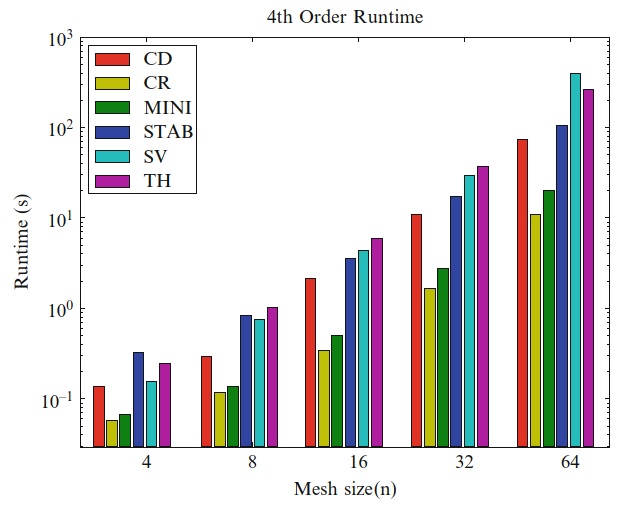
图20.15

图20.15 分析测试用例的运行时。除Crouzeix-Raviart和MINI以外，所有速度空间均为四阶，压力空间由该方法确定。Crouzeix–Raviart和MINI是在细网格上计算的，其自由度与四阶Taylor–Hood方法相似。 CR，TH和SV分别指Crouzeix–Raviart，Taylor–Hood和Scott–Vogelius。

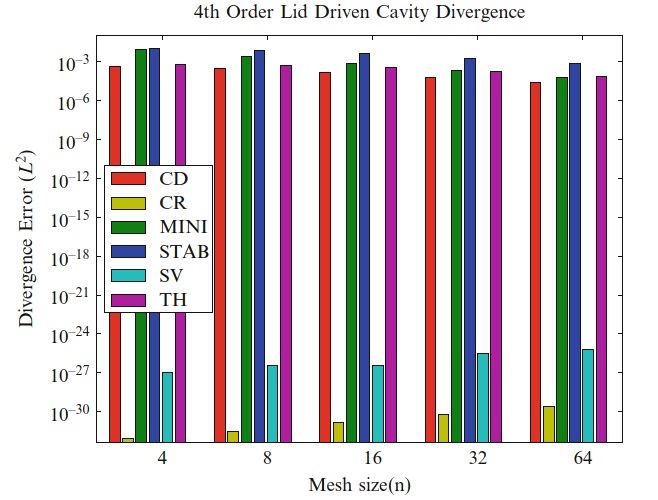
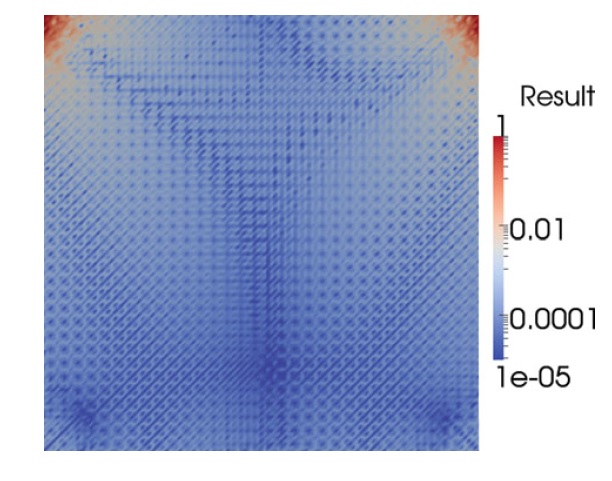
图20.16显示了盖驱动腔问题的速度散度的 $$L^2$$ 范数。与已经考虑过的平滑测试用例不同，CD，MINI，STAB和Taylor-Hood单元的散度误差不会随着网格细化而减小。在盖角上的压力奇异点周围仍然存在散度误差，如图20.17中的Taylor-Hood情况所示。为了用Scott-Vogelius方法解决盖驱动腔问题，必须将惩罚参数增加到1×108，以使固定点迭代收敛。

图20.16

图20.16 盖驱动腔测试问题的散度误差。

图20.17

图20.17 使用P2-P1 Taylor-Hood单元的盖驱动腔中的局部散度误差。尤其要注意在盖子角落处的较大误差。

20·5 结论

提出了Stokes问题的不同有限元之间的比较。通过自动生成各种方法的求解器，已经证明了自动代码生成提供的灵活性。在所有情况下观察到的收敛速度与先验估计一致。在所检查过的单元中，Crouzeix-Raviart单元和Scott-Vogelius导致的散度误差最小，而Taylor-Hood的速度误差最小。如果质量守恒特性不是至关重要的，那么Taylor–Hood或STAB等单元的简单性就很有吸引力。

【章节目录】