Unicorn:统一的连续介质力学求解器(下)【翻译】
【章节目录】
18·5 解决连续介质力学问题
在本节中,我们介绍一些使用Unicorn计算的示例。 第一个例子是没有自适应性的流固耦合问题,我们讨论了几何和子域的建模,系数(形式中使用的函数),主程序的参数和规范(运行求解器的接口)。 接下来,我们给出一个用自适应性解决湍流纯流体问题的示例,其中我们涵盖了对偶问题的数据建模,自适应回路,并指定了用于建模湍流边界层的滑移/摩擦边界条件。
我们在这里介绍了问题实现的示例性片段。 有关完整的详细信息,请参见Unicorn源代码分发。
18·5·1 流固耦合
我们在这里给出解决流固连续介质力学问题的用例,其中用户指定了用于建模问题的数据,并描述了接口和预期结果。 问题在于(Hron和Turek,2005年)给出的FLUSTRUK-A变体3基准,并在(Hoffman等人,2011年)以及第28章中用作Unicorn的验证。 在时间
\(t = 1\)
和
\(t = 5.5\)
时,速度场和相函数
\(\theta\)
绘制在图18.16中。 完整示例可以在Unicorn发行版unicorn-0.1.3-hpc/ucsolver/fsi/cylinder2D/下找到。

我们将用例分为四个部分:
几何和子域
用户指定可能的几何参数并定义子域。 我们注意到,对于复杂的几何,用户可以省略几何信息,并将子域标记指定为数据文件。
系数
声明了已知的系数(在形式中出现的函数),例如力函数和边界条件。
参数
在参数文件中给出了指定材料属性和数值公差的简单参数。
主程序
用户实现主程序,并声明数据并将其传递给求解器。
这四个部分通过图18.18–18.21中显示的代码示例展示。
18·5·2 自适应性
我们继续用一个纯流体湍流问题自适应解的用例:环绕3维立方体的流动,该立方体对应于第28章中给出的立方体问题描述。 该解的快照可以在图18.17中看到。 完整示例可在Unicorn发行版的unicorn-0.1.3-hpc/ucsolver/icns/cube/下找到。

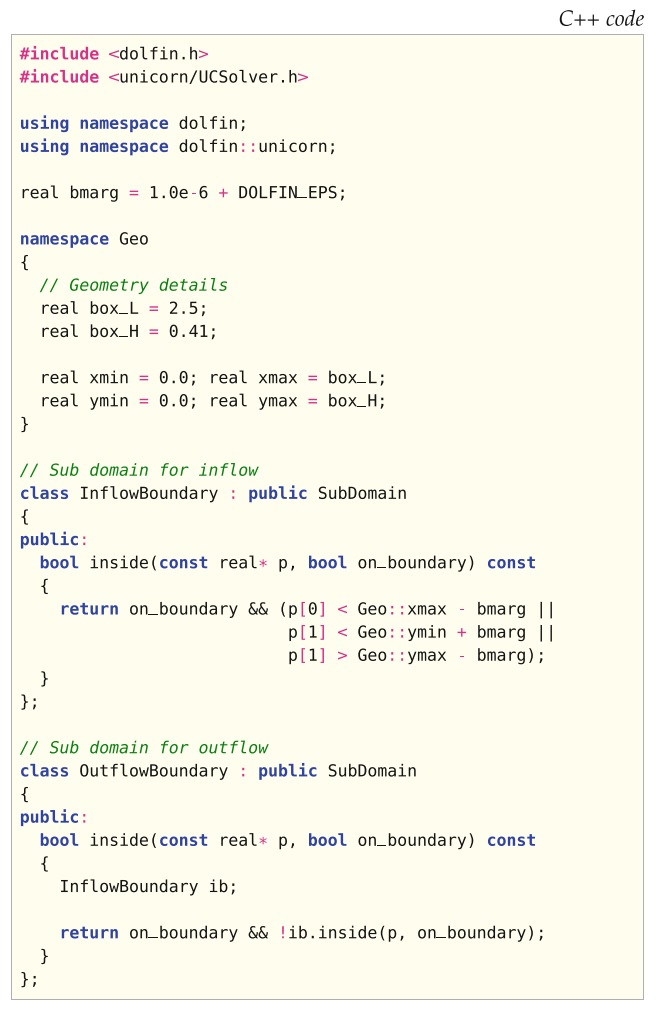
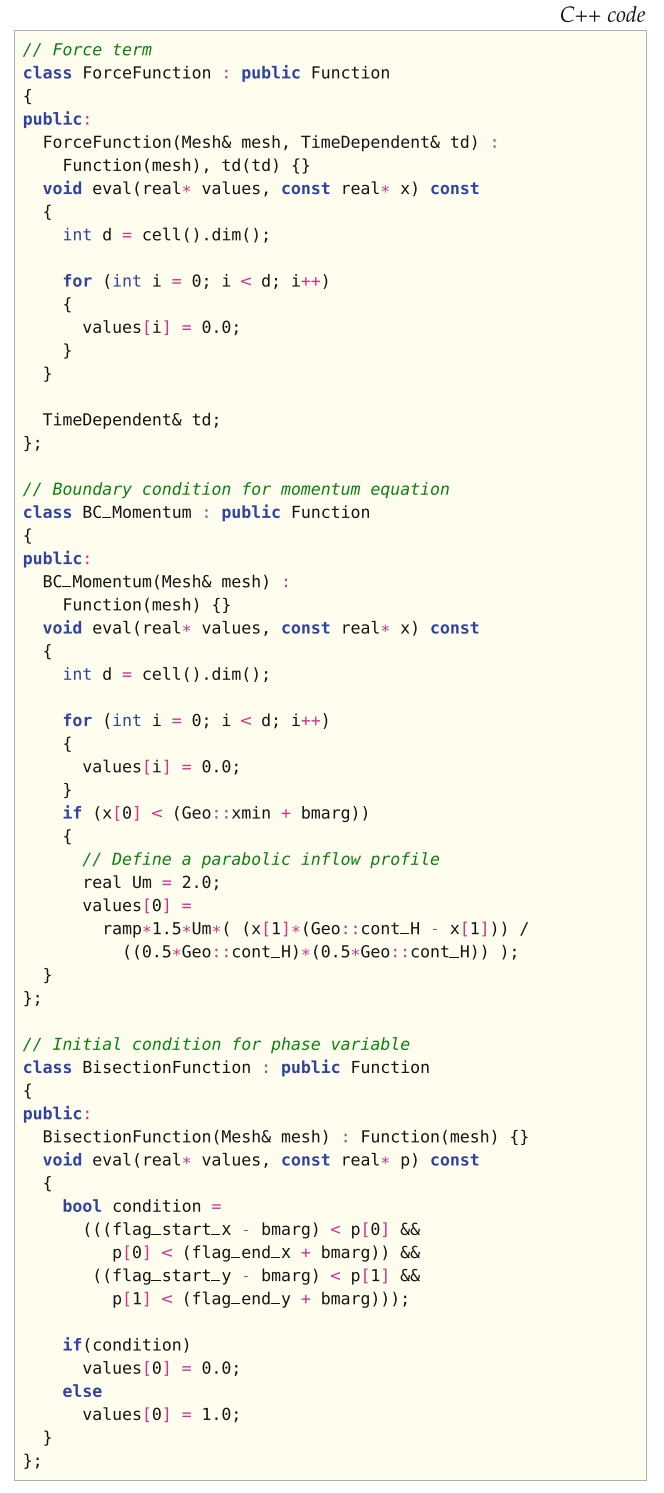


问题的实现与流固的情况非常相似(仅使用纯流体数据),但有3个重要的补充:
对偶问题
为了计算自适应算法所需的误差估计,我们必须求解由原始问题产生的对偶问题和输出量 \(\psi\) 。 由于对偶问题在形式上与原始问题相似,因此我们将两者都实现为同一求解器的变体。 在这种情况下,我们对计算阻力感兴趣,将 \(\psi\) 作为对偶问题的边界条件:
自适应回路
我们指定一个solve()函数,该函数计算自适应循环的一次迭代:求解原始问题,求解对偶问题,计算误差估计并检查是否满足公差并计算自适应网格。 此函数在unicorn_solve()函数中的自适应循环中被调用。
class Dual_BC_Momentum : public Function
{
public:
Dual_BC_Momentum(Mesh& mesh) : Function(mesh) {}
void eval(real* values, const real* x) const
{
values[0] = -1.0;
values[1] = 0.0;
values[2] = 0.0;
}
};
solve()
{
// Boundary condition for dual problem
CubeBoundary cb;
Dual_BC_Momentum dual_bcf_mom(mesh);
DirichletBC dual_bc0(dual_bcf_mom, mesh, cb);
Array <BoundaryCondition*> dual_bc_mom;
dual_bc_mom.push_back(&dual_bc0);
...
// Solve primal problem
NSESolver primal_solver(mesh, node_normal, f, beta, aero_f,
primal_bc_mom, primal_bc_con, chkp, w_limit, td, "primal");
primal_solver.solve();
// Solve dual problem (gives weight for error estimate)
NSESolver dual_solver(mesh, node_normal, f, beta, aero_f, dual_bc_mom,
dual_bc_con, chkp, w_limit, td, "dual");
dual_solver.solve();
}
滑移边界条件
对于湍流,我们将边界层建模为摩擦边界条件。 我们将法向分量指定为与常规Dirichlet边界条件相同的强滑动边界条件。
NodeNormal node_normal(mesh);
SlipBoundary sb;
SlipBC slip_bc(mesh, sb, node_normal);
Array <BoundaryCondition*> primal_bc_mom;
primal_bc_mom.push_back(&slip_bc);
18·5·3 Unicorn-HPC安装和基本测试
Unicorn-HPC是Unicorn的高性能计算分支,并且是积极开发的分支。 与本书各章相对应的版本是“ Unicorn 0.1.3-hpc”。 对于以前发表的文章中引用的模拟和绘图,我们参考该特定文章以获取软件详细信息。 当前,Unicorn的MAdLib网格自适应接口仅在不再维护的Unicorn串行分支中可用,我们在Live DVD unicorn_fenics-book.iso中提供了该分支,可通过以下任一方式获得 http://www.csc.kth.se/ctl or http://fenicsproject.org.
要验证Unicorn-HPC的正确安装和功能,请遵循Unicorn-HPC发行版中“测试”下自述文件中的步骤。 该测试代表了第28章及更高版本中描述的环绕立方体模拟的湍流。
18·6 致谢
我们感谢以下公司对Unicorn的贡献,软件开发以及思想和科学支持:Mattias Aechtner,Peter Brune,Zilan Ciftci,GéetanCompere,Claes Johnson,Ashraful Kadir,KasparMüller,JeannetteSpühler,MichaelStöckli和Rodrigo Vilela de Abreu。
作者要感谢欧洲研究委员会,瑞典战略研究基金会,瑞典研究委员会和瑞典能源署的财政支持。 这些模拟是由瑞典国家基础设施计算中心(SNIC),高性能计算中心北部(HPC2N),瑞典国家超级计算机中心(NSC)和PDC –高性能计算中心提供的资源执行的。
【章节目录】