Unicorn：统一的连续介质力学求解器（中）【翻译】

2021-02-19

| 科学计算 | | FEniCS , 有限元法 , 偏微分方程 |

18·4 实现

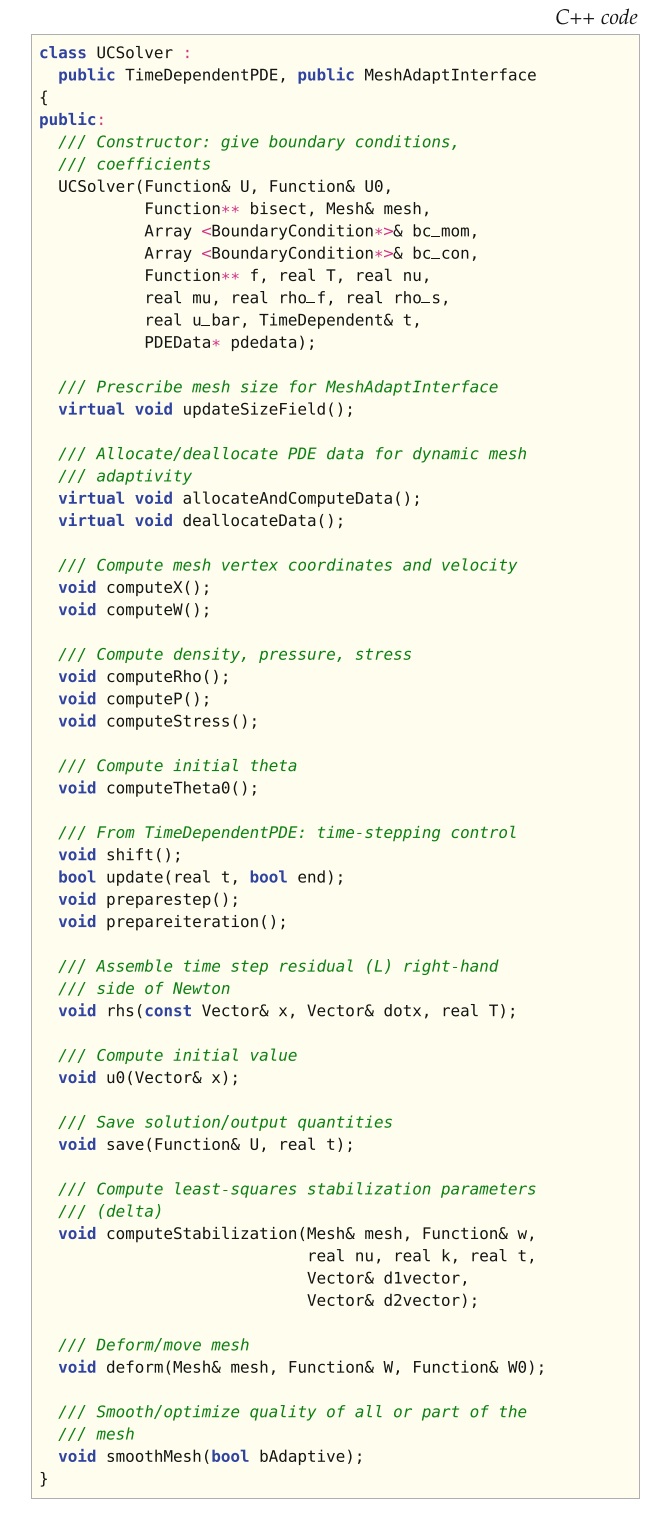
在这里，我们概述了Unicorn的设计。 Unicorn求解器类UCSolver将Unicorn库中的技术与FEniCS的其他部分结合，合在一起公开一个接口（请参见清单18.6），以模拟连续介质力学中的应用。求解器实现的主要部分是UC模型的G2离散化的弱形式（请参见图18.4），以及用于误差估计的应力和残差的形式。来自应用程序的系数被连接到形式，然后由TimeDependentPDE类执行时间步进。某些系数，例如 $\delta$ 稳定化系数，也作为求解器的一部分（而不是作为形式）来进行计算。求解器计算自适应算法的一次迭代（主求解，对偶求解和网格划分），其中，自适应循环是通过迭代运行一系列网格的求解器来实现的。

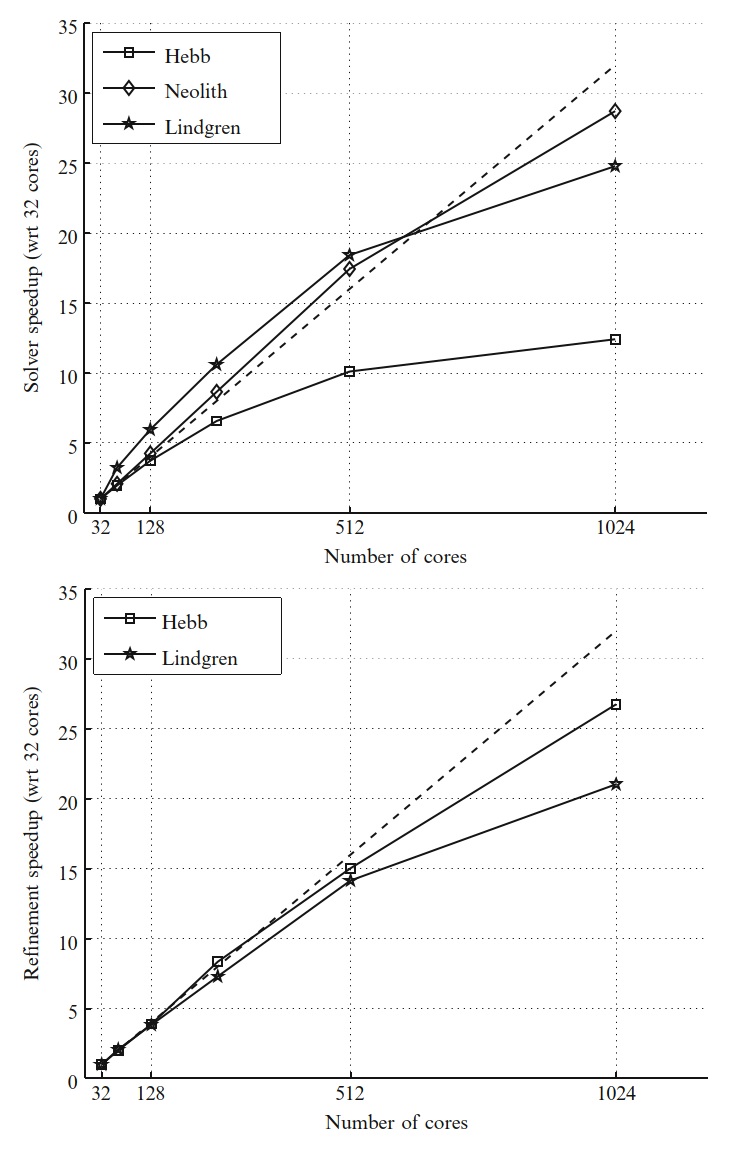
对于使用MPI的分布式内存体系结构，UCSolver已经实现并行化，我们可以在多个平台上展示数百个内核的强大扩展能力（见图18.5）。整个自适应算法是并行的，包括Rivara网格修正和先验预测负载平衡。 Unicorn可以有效地模拟不可压缩的湍流的大规模并行应用（Jansson等，2010； Jansson，2011）。图18.3给出了并行自适应圆柱体仿真的示例。

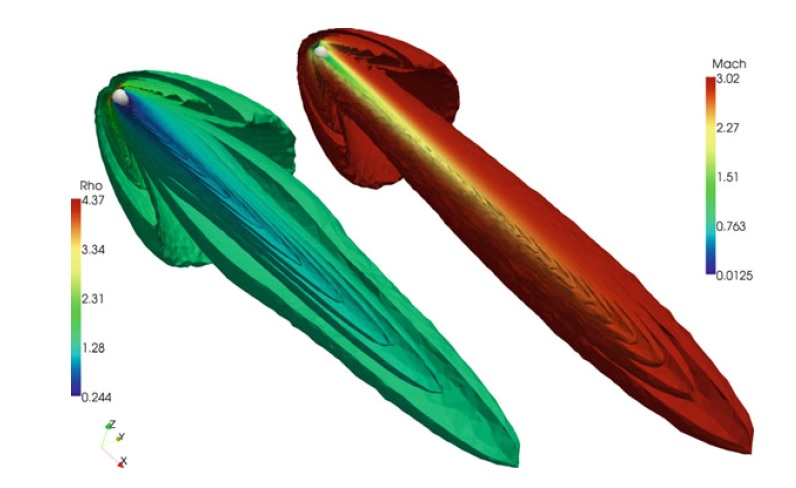
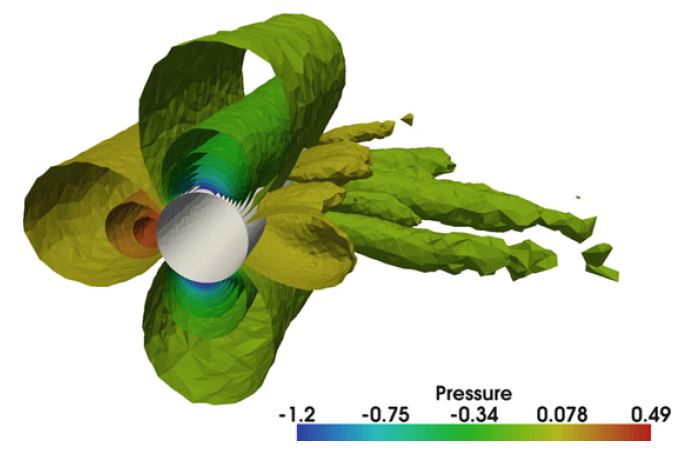
UCSolver的一个可压缩变体CNSSolver，用于适应G2的可压缩Euler流。除了不可压缩性之外，更一般方法和算法与UCSolver的方法和算法非常接近。长期目标是统一不可压缩/可压缩的表述。关于可压缩CNSSolver的实现细节，请参阅Nazarov（2009）。有关球体周围可压缩流的示例图，请参见图18.2。

图18.2

图18.2 围绕球体的3维可压缩流的自适应计算的示例应用。

图18.3

图18.3 具有并行自适应计算的圆柱体周围3维不可压缩湍流的示例应用。

图18.4

图18.4 用于求解不可压缩的UC模型的牛顿迭代（近似雅可比）的双线性和线性形式的源代码。

图18.5

图18.5 在几种不同的体系结构上，网格细化和整个求解器具有强大的伸缩结果：Lindgren（Cray XT6m），Hebb（BlueGene / L）和Neolith（带有InfiniBand的常规Linux群集）。虚线表示理想的加速。

图18.6

图18.6 Unicorn的类UCSolver的C++类接口。

18·4·1 Unicorn类／接口

以下类/接口中提供了关键概念的抽象：

TimeDependentPDE: 时间步进

在每个时间步中，非线性代数系统都通过不动点迭代来求解。

ErrorEstimate: 自适应误差控制

适应性是基于计算形式 $\eta_K = \|hR(U)\|_T\|DZ\|_T$ 的局部误差指标，其中 $$Z$$ 是所谓的对偶解。

SpaceTimeFunction: 时空系数

时空函数/系数的存储和求值。

SlipBC: 摩擦边界条件

Unicorn中湍流的有效计算是基于通过摩擦模型对湍流边界层进行建模的，其中滑移边界条件 $u \cdot n = 0$ 作为代数系统的一部分而得到了强有力的实现。

ElasticSmoother: 弹性网格平滑/优化

根据弹性类比的胞元质量优化。

MeshAdaptInterface: 网格自适应接口

使用本地网格操作对MAdLib软件包的接口进行抽象以进行网格自适应。

18·4·2 TimeDependentPDE

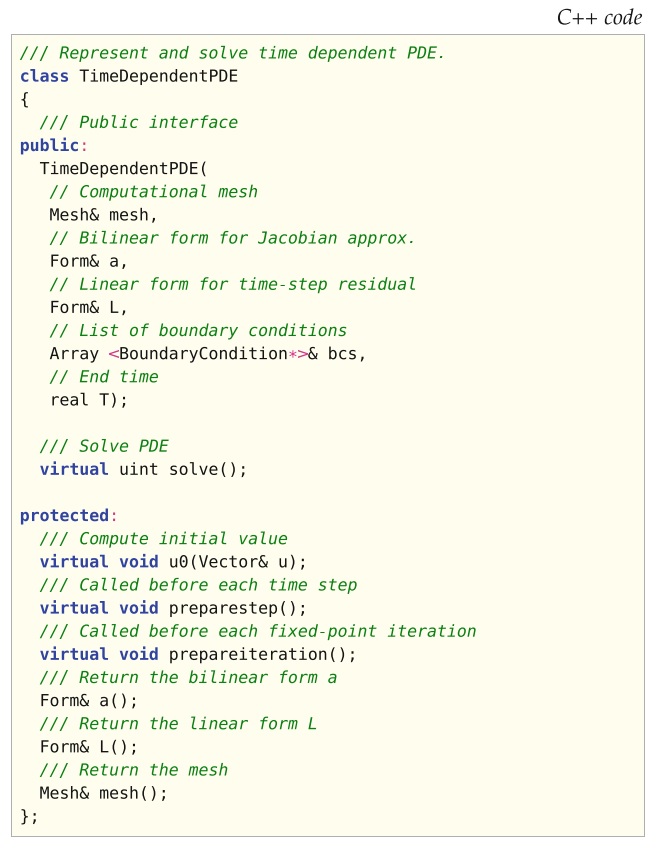
我们考虑比如 $\frac{\partial}{\partial t} u + A(u) = 0$ 的一般时间依赖方程，其中 $$A$$ 表示空间中可能的非线性微分算符。我们想定义一个类（数据结构和算法）来抽象G2方法的时间步进。该方程作为输入给出，时间步进应自动生成。我们对于cG(1)cG(1)方法通过应用简化的牛顿法做到这一点。它封装在图18.7的C++类接口中，称为TimeDependentPDE。

图18.8实现了带不动点迭代的时间步进骨架。

图18.7

图18.7 TimeDependentPDE的C++类接口。

图18.8

图18.8 在Unicorn中使用不动点迭代实现时间步进的骨架。

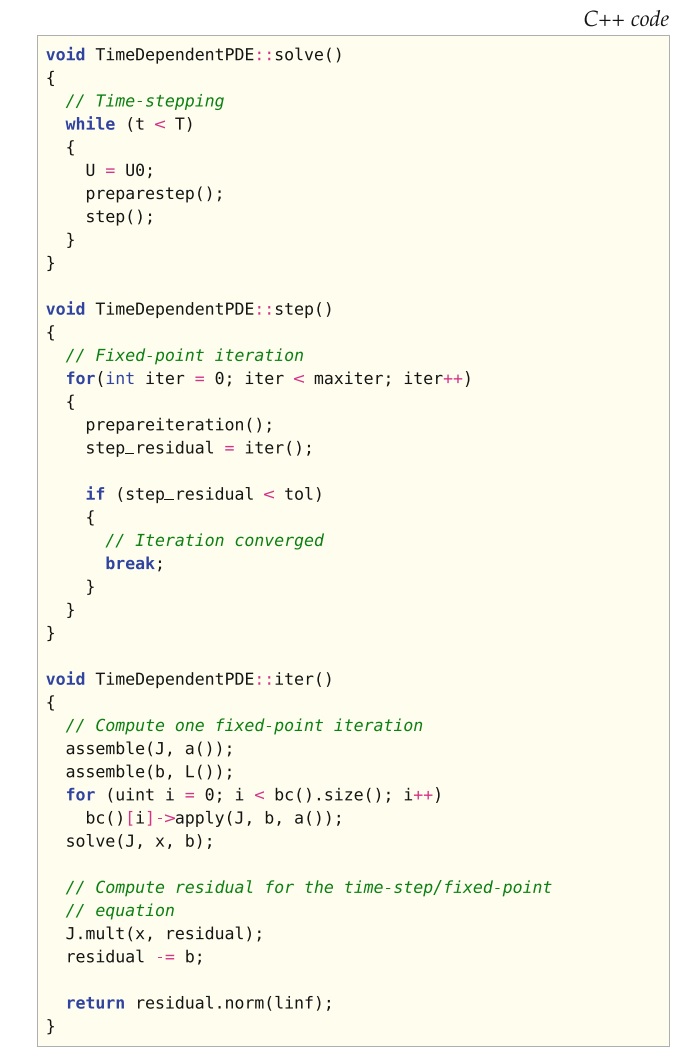
我们使用块对角准牛顿法，从公式完整的牛顿法开始，然后将各项从对角块中删除。我们还使用本构定律作为恒等式来表示 $$U$$ 各项中的 $\Sigma$ ，与通过在 $\Sigma$ 和 $$U$$ 之间进行迭代相比，可以允许更大的时间步长。参见Jansson（2009）；Hoffman等（2011年）了解更多详细信息，并讨论了不动点迭代及其实现的效率。

18·4·3 ErrorEstimate

基于对偶的自适应误差控制算法需要以下组件：

残差计算 我们通过分段常数空间中的 $$L^2$$ -投影，计算残差 $$R(U)$$ 在每个胞元中的平均值。

对偶解 我们使用与原始问题相同的技术来计算对偶问题的解。对偶问题虽然在时间上是向后求解的，但通过时间坐标变换 $$s = T - t$$ ，我们可以使用标准的TimeDependentPDE接口。

时空函数存储/求值 我们在计算对偶问题的同时计算误差指标，作为对胞元的时空积分： $\eta_T=\left\langle R(U)\ ,\ \frac{\partial}{\partial x}Z\right\rangle$ ，在这里我们需要对原始解 $$U$$ 和对偶解 $$Z$$ 进行求值。 $$U$$ 是对偶方程的系数。这需要存储并对时空函数求值，该函数封装在SpaceTimeFunction类中。

自适应网格 计算误差指标后，我们选择指标最大的 $p\%$ 进行细化。然后通过递归Rivara胞元二等分法进行优化。或者，可以使用MAdLib（Compère等人，2009）进行基于边缘拆分，折叠和交换的更通用的网格自适应操作。

使用这些组件，我们可以构建自适应算法。自适应算法封装在图18.9中的C++类接口ErrorEstimate。

图18.9

图18.9 C++类接口ErrorEstimate。

18·4·4 SpaceTimeFunction

作为解决对偶问题的一部分，误差估计算法需要对在对偶问题定义中出现的时空系数进行求值。特别是，我们必须对原始解 $$U$$ 在时间 $$s=T-t$$ 处求值。这需要存储和求值一个时空函数，封装在SpaceTimeFunction类中（请参见图18.10）。

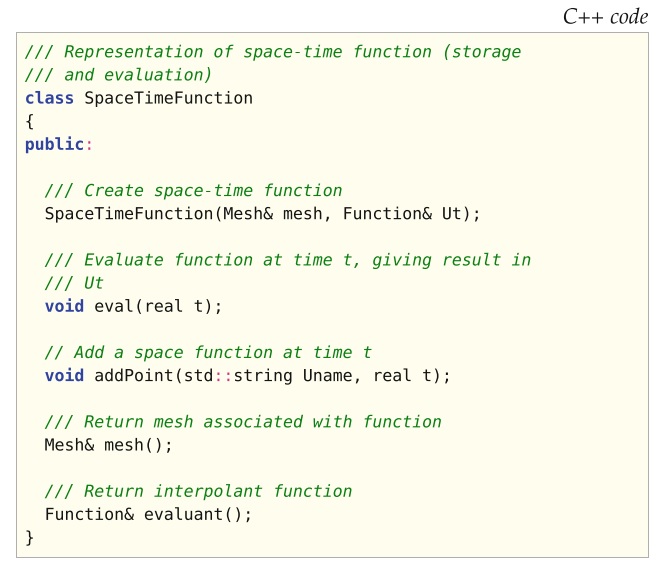
图18.10

图18.10 C++类接口SpaceTimeFunction。

时空泛函被实现为在常规采样时间的空间函数列表，对其求值是时间自由度的分段线性插值。

18·4·5 SlipBC

对于雷诺数较高的问题，例如汽车的空气动力学或飞机的飞行能力，无法解决湍流边界层。然后，一种可能性是通过摩擦模型来建模湍流边界层：

u \cdot n = 0 \tag{18.18}

\beta u \cdot \tau_k + (\sigma n) \cdot \tau_k = 0\qquad k = 1, 2 \tag{18.19}

我们实现了法向分量条件（滑移）的强边界条件。这里的“强”是指在代数系统中将左侧矩阵和右侧向量组合后的边界条件实现，而切向分量（摩擦）是通过在变分公式中添加边界积分的“弱”实现。找到与自由度相对应的矩阵行和荷载向量，并根据边界条件用新行替换。

想法如下：最初，测试函数 $$v$$ 以笛卡尔标准基底 $$(e_1, e_2, e_3)$$ 表示。现在，将测试函数以 $(n, \tau_1, \tau_2)$ 为基底局部映射到法向-切向坐标，其中 $$n = (n_1, n_2, n_3)$$ 为法向，而 $\tau_1 = (\tau_{11}, \tau_{12}, \tau_{13})$ ， $\tau_2 = (\tau_{21}, \tau_{22}, \tau_{23})$ 是边界上每个节点的切向。这使我们可以限制法向，而切向自由：

v = (v \cdot n)n + (v \cdot \tau_1)\tau_1 + (v \cdot \tau_2)\tau_2 \tag{18.20}

对于矩阵和向量，这意味着对应于边界行需要分别乘以 $n, \tau_1, \tau_2$ ，然后将速度的法向分量设置为零。

此概念封装在SlipBC类中，该类是dolfin::BoundaryCondition的子类，用于表示强边界条件。有关滑移边界条件实现的更多详细信息，请参见Nazarov（2011）。

18·4·6 ElasticSmoother

为了在UC模型中保持不连续相界面，我们将网格速度 $\beta_h$ 定义为固相中的离散速度 $$U$$ （特别是在界面上）。流体中的网格速度可以任意选择，但必须满足网格质量和尺寸标准。我们构造基于UC的纯弹性变体的胞元质量优化/平滑方法（请参见图18.11中的形式）。对于网格速度 $\beta_h$ ，我们定义了以下要求：

在网格的固相部分中， $\beta_h=U$ 。
有界网格质量 $$Q$$ 定义为 $Q =\frac{d\|F\|^2_F}{\det(F)^{\frac{d}{2}}}$ 其中， $$d$$ 是空间维度，在网格的流体部分。最好是，如果可能的话，网格平滑应该能改善 $$Q$$ 。
在自适应算法中，保持网格尺寸 $$h(x)$$ 接近所需的后验误差估计所给定的 $\hat{h}(x)$ 。

图18.11

图18.11 表示UC模型的弹性平滑变体中变形梯度（

\(F\)

）演化的一个时间步的形式的源码。

在Unicorn中，通过使用本构定律 $\sigma = \tau(I − (FF^T)^{−1})$ 的弹性模型处理网格平滑，我们将 $$F$$ 称为变形梯度。我们使用更新定律： $\frac{\partial}{\partial t} F^{−1} = −F^{−1}\nabla u$ ，因此我们需要F的初始条件。我们设置初始条件 $F_0 = \bar{F}$ ，其中 $\bar{F}$ 是关于等边参考胞元的变形梯度，代表质量 $$Q = 1$$ 的最佳形状。

因此，求解弹性模型可以看作是针对网格中最高的全局质量 $$Q$$ 进行优化。对于低质量的胞元，我们还在杨氏模量 $\mu$ 上引入权重，这会损害较高的平均水平，但会导致局部质量低于中等水平的全局质量。我们参考源代码以获取更多详细信息。

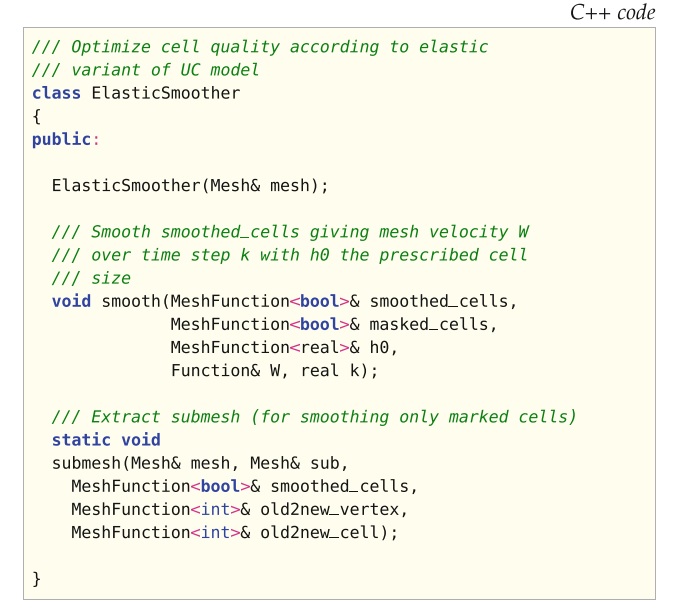
Unicorn提供了ElasticSmoother类（请参见图18.13，该类可用于平滑/优化整个或部分网格的质量）。

我们对弹性平滑度和网格自适应性进行了鲁棒性测试，如图18.12所示，其中我们使用与湍流3D标记问题相同的几何形状，但是定义了零流速，并且向标记添加了重体积力，以创建标记指向下方时发生大变形。弹性平滑和网格自适应都可以计算解，但是正如预期的那样，弹性网格平滑最终无法控制胞元质量；在限定胞元质量的同时，还不存在可以处理较大的刚体旋转的网格运动。

图18.12

图18.12 （a）弹性平滑和（b）网格自适应的鲁棒性测试。请注意，变形不好的胞元被挤压在立方体和标记之间。

图18.13

图18.13 C++类接口ElasticSmoother.

18·4·7 MeshAdaptInterface

如上所述，自适应算法中的关键要素是网格自适应性，我们将其定义为构造满足给定网格尺寸函数 $$h(x)$$ 的网格。

我们从介绍Rivara递归二等分算法（Rivara，1992）开始，这是网格自适应性的基本选择（当前是并行网格自适应性的唯一可用选择），但是只能细化而不是粗化。然后，提出了更通用的MAdLib，它可以通过局部网格操作（边分割，边折叠和边交换）来对指定的 $$h(x)$$ 进行全网格自适应。

Rivara递归二等分 Rivara算法将胞元的最长边一分为二（拆分），从而用两个新胞元替换该胞元，并使用递归对分法消除带有悬挂节点的不合格胞元。相同的算法在2D/3D（三角形/四面体）中均适用。在2D模式下，可以证明（Rivara，1992），该算法以有限的步长终止，并且已细化的网格最小角度至少是起始网格最小角度的一半。在实践中，该算法可以在2D和3D中生成质量优良的细化网格。

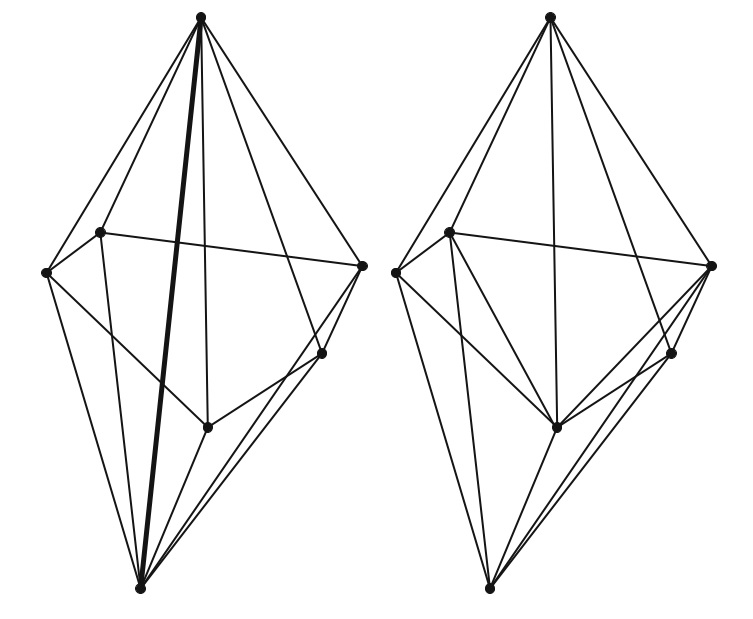
局部网格操作: MAdLib MAdLib结合了网格自适应算法和实现，其中定义了一小组局部网格修改操作，例如边分割，边折叠和边交换（有关边交换操作的说明，请参见图18.14）。定义了一种网格自适应算法，在控制回路中使用这组局部操作来满足规定的尺寸场 $$h(x)$$ 和质量公差。边交换是提高胞元质量的关键操作，例如在具有大量连接边的顶点周围。

在有限元方法的表述中，通常假设可以自由修改计算网格的胞元大小，以满足所需的尺寸场 $$h(x)$$ 或允许网格运动。在最先进的有限元软件实现中，很少出现这种情况（Bangerth等，2007； COMSOL，2009）。

MAdLib中的网格自适应算法提供了使用局部网格操作来适应指定尺寸场的自由。该实现以免费/开源软件的形式发布.

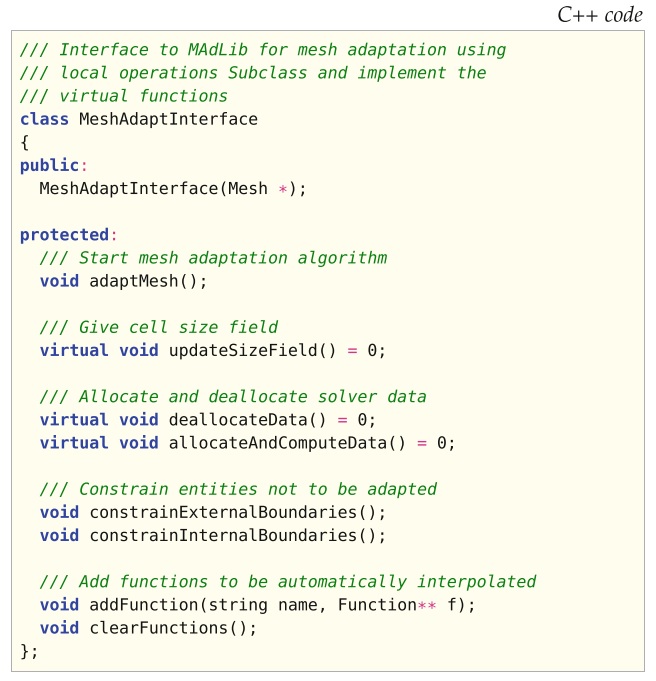
Unicorn提供了MeshAdaptInterface类（请参见图18.15），在该类中可以使用MAdLib子类化并实现虚拟函数来控制网格自适应。

图18.14

图18.14 边交换操作：（顶部）初始腔体，突出显示交换边，（底部）交换之后可能的配置。

图18.15

图18.15 C++类接口MeshAdaptInterface.

【章节目录】