UFL：有限元形式语言》形式算符&表达式的表示【翻译】

2021-02-02

| 科学计算 | | FEniCS , 有限元法 , 偏微分方程 |

17·5 形式算符

一旦定义了一些形式，就有几种方法可以从中计算相关的形式。上节的算符可用于定义表达式，本节中讨论的算符被用于形式，从而生成新的形式。形式算符既可以使形式的定义更紧凑，又可以减少错误的可能，因为原始形式中的更改将自动传播到根据它所计算出的形式中。这些形式算符可以任意组合；给定一个半线性形式，只需要几条行即可计算出雅可比伴随的作用。由于这些计算是在形式编译器处理之前完成的，因此在运行时没有任何开销。

17·5·1 形式的微分

形式算符derivative声明了一个形式关于离散函数系数（Coefficient）的导数。例如，可以使用此功能结合Newton-Raphson方法，自动将您的非线性残差方程（线性形式）线性化。它也可以被多次应用，这对于从凸函数导出线性系统很有用，以便找到使泛函最小化的函数。对于非平凡方程，手工计算这些表达式可能很繁琐。此功能可能对其他领域也是有用的，包括最优控制和反演理论，以及灵敏度分析。

就简单的形式，声明形式 $$L$$ 关于系数函数 $$w$$ 的导数：

# UFL code
a = derivative(L, w, u)

形式 $$a$$ 取决于附加的基函数参数 $$u$$ ，该参数必须与函数 $$w$$ 位于相同的有限元空间中。如果省略最后一个参数，则会创建一个新的基函数参数。

让我们逐步介绍一个示例，如何对泛函求导两次，进而导出一个线性系统。在下文中， $$V_h$$ 是具有基底的有限元空间， $$w$$ 是 $$V_h$$ 中的函数，而 $$f = f (w)$$ 是我们要最小化的泛函。从 $$f (w)$$ 导出的是线性形式 $$F(w; v)$$ 和双线性形式 $$J(w; u, v)$$ 。

V_h = \mathrm{span} \{\phi_k\} \tag{17.52}

w(x) =\sum^{|V_h|}_{k=1}w_k \phi_k(x) \tag{17.53}

f : V_h \to \mathbb{R} \tag{17.54}

F(w; \phi_i) =\frac{\partial f (w)}{\partial w_i} \qquad i = 1, \dots , |V_h| \tag{17.55}

J(w; \phi_j, \phi) =\frac{\partial F(w; \phi)}{\partial w_j} \qquad j = 1, \dots , |V_h|, \phi \in V_h \tag{17.56}

对于具体的泛函 $f (w) = \int_\Omega \frac{1}{2} w^2 dx$ ，我们可以将其实现为

# UFL code
v = TestFunction(element)
u = TrialFunction(element)
w = Coefficient(element)
f = 0.5*w**2*dx
F = derivative(f, w, v)
J = derivative(F, w, u)

此代码声明两种形式F和J。线性形式F表示标准载荷矢量w*v*dx，双线性形式J表示质量矩阵u*v*dx。

也可以是关于有限元混合空间函数的系数的求导。考虑从泛函导出的调和映射方程

f (x, \lambda) = \int_\Omega \left(\mathrm{grad} \ x : \mathrm{grad} \ x + \lambda x \cdot x\right) dx \tag{17.57}

其中， $$x$$ 是向量有限元空间 $$V_h^d$$ 中的函数，而 $\lambda$ 是标量有限元空间 $$V_h$$ 中的函数。从等式17.57中的泛函导出的线性和双线性形式，有属于混合空间 $V_h^d\times V_h$ 中的基函数参数。可通过自动线性化来得到这些形式

# UFL code
Vx = VectorElement("Lagrange", triangle, 1)
Vy = FiniteElement("Lagrange", triangle, 1)
u = Coefficient(Vx*Vy)
x, y = split(u)
f = inner(grad(x), grad(x))*dx + y*dot(x,x)*dx
F = derivative(f, u)
J = derivative(F, u)

注意，该泛函通过两个子函数 $$x$$ 和 $$y$$ 来表示，而derivative的参数必须是单个混合函数 $$u$$ 。在此示例中，derivative的基函数参数被省略，因此自动由正确的函数空间中提供。

请注意，在计算形式的导数时，我们假设

\frac{\partial }{\partial w_k} \int_\Omega I dx = \int_\Omega \frac{\partial}{\partial w_k} I dx \tag{17.58}

或更特别地，域 $\Omega$ 与 $$w$$ 无关。同样，除 $$w$$ 以外的任何系数都被认为与 $$w$$ 无关。此外，请注意，在此框架中对单元的选择没有任何限制，特别是支持任意混合单元。

17·5·2 伴随

另一个形式算子是双线性形式 $$a$$ 的伴随 $$a^*$$ ，定义为 $$a^*(v, u) = a(u, v)$$ ，等效于组装成稀疏矩阵后再进行转置。在UFL中，这可以简单地通过交换测试函数和试探函数的顺序来实现，并且可以使用形式算符adjoint。（请注意，这不是伴随算符的最一般的定义）。在各向异性扩散项上使用它的一个例子看起来像

# UFL code
V = VectorElement("Lagrange", cell, 1)
T = TensorElement("Lagrange", cell, 1)
u = TrialFunction(V)
v = TestFunction(V)
M = Coefficient(T)
a = M[i,j]*u[k].dx(j)*v[k].dx(i)*dx
astar = adjoint(a)

对应于（ $u\in U$ 和 $v\in V$ ）

a(M; u, v) =\int_\Omega M_{ij} u_{k,j} v_{k,i} dx \tag{17.59}

a^∗(M; v, u) =\int_\Omega M_{ij} u_{k,j} v_{k,i} dx = a(M; u, v) \tag{17.60}

如果我们需要使用求导来计算非对称双线性形式的伴随，那么这种自动转换特别有用，因为 $$a$$ 的显式表达式并不在其间。与derivative结合使用时，以下几种形式算符最有用。

17·5·3 替换函数

通过使用其他值替换终端对象，可以使用新定义的形式参数来对形式求值。假定您已经定义了依赖于某些函数 $$f$$ 和 $$g$$ 的形式 $$L$$ 。然后，您可以通过将这些函数替换为其他函数或固定值，来得到特定形式，比如

L(f , g; v) = \int_\Omega \frac{f^2}{2g}v\ dx \tag{17.61}

L_2(f , g; v) = L(g, 3; v) = \int_\Omega \frac{g^2}{6}v\ dx \tag{17.62}

此功能通过replace实现了，如下所示：

# UFL code
V = FiniteElement("Lagrange", cell, 1)
v = TestFunction(V)
f = Coefficient(V)
g = Coefficient(V)
L = f**2 / (2*g)*v*dx
L2 = replace(L, { f: g, g: 3})
L3 = g**2 / 6*v*dx

L2和L3代表完全相同的形式。由于它们仅取决于g，为这些形式生成的代码可以更高效。

17·5·4 作用

在某些应用中，不明确需要矩阵，而只需要矩阵对矢量的作用。直接组装结果向量，先比组装稀疏矩阵然后执行矩阵-向量乘法要有效得多。假设 $$a$$ 是双线性形式， $$w$$ 是定义在与 $$a$$ 中试探函数相同的有限元上的系数。令 $$A$$ 表示可以从 $$a$$ 组装的稀疏矩阵。然后，您可以通过定义代表双线性形式 $$a$$ 作用于一个函数 $$w$$ 的线性形式 $$L$$ ，进而直接将其组装成 $$A$$ 对向量的作用。简单地表示成L = action(a, w)，甚至缩写为L = a*w。

17·5·5 系统分割

如果您更喜欢将PDE的所有项都写在一侧，比如

a(u, v) − L(v) = 0 \tag{17.63}

您可以同时声明线性项和双线性项，然后将方程拆分为 $$a$$ 和 $$L$$ 。一个简单的例子是

# UFL code
V = FiniteElement("Lagrange", cell, 1)
u = TrialFunction(V)
v = TestFunction(V)
f = Coefficient(V)
pde = u*v*dx - f*v*dx
a, L = system(pde)

这里的system用于将PDE分为双线性和线性部分。或者，可以使用lhs和rhs分别获得这两个部分。记住，线性部分的结果符号，对应于在公式（17.63）中将L移动到右侧。

17·5·6 计算函数的敏感性

如果您找到了方程（17.63）的解 $$u$$ ，并且 $$u$$ 依赖于某个标量常值 $$c$$ ，则可以计算 $$u$$ 关于 $$c$$ 的变化灵敏度。如果 $$u$$ 被表示成代数线性系统 $$Ax = b$$ 解的系数向量 $$x$$ ，那么 $\frac{\partial u}{\partial c}$ 的系数就是 $\frac{\partial x}{\partial c}$ 。将 $\frac{\partial}{\partial c}$ 应用于 $$Ax = b$$ 并使用链式规则，我们可以写成

A \frac{\partial x}{\partial c}=\frac{\partial b}{\partial c}−\frac{\partial A}{\partial c} x \tag{17.64}

因此，可以通过求解相同的代数线性系统算出的 $$x$$ 来发现 $\frac{\partial x}{\partial c}$ ，仅在右侧不同。可以写出与等式（17.64）右边相对应的线性形式

# UFL code
u = Coefficient(element)
sL = diff(L, c) - action(diff(a, c), u) # 执行报错，我尚未做到原因

或者您可以使用等效的形式转换

# UFL code
sL = sensitivity_rhs(a, u, L, c) # 执行报错，我尚未做到原因

请注意，解 $$u$$ 必须用Coefficient表示，而 $$a(u, v)中$$ 的 $$u$$ 用Argument表示。

17·6 表达式的表示

从高级的角度来看，UFL就是形式的定义。每种形式都包含一个或多个标量被积表达式，但是形式表示在很大程度上与被积表达式的表示无关。实际上，UFL实现的大多数复杂性都与表达式的表示，表现和操纵有关。本章的其余部分将重点介绍表达式的表示以及在其上操作算法。这些主题对UFL的普通用户几乎没有兴趣，而更多地针对开发人员和好奇的面向技术的用户。

为了在没有实现细节负担的情况下推理表达式算法，我们需要对表达式结构进行抽象表示。 UFL表达式是程序的表示，并且该表示法应使我们能够看到这种联系。下面，我们将根据这种抽象符号来讨论表达式的属性，并与特定的实现细节相关。

17·6·1 表达式的结构

不依赖于其他表达式的最基本的表达式称为终端表达式。将某些算符应用于一个或多个现有表达式会产生其他表达式。考虑任意（非终端）表达式 $$z$$ 。该表达式依赖于一组终端表达式 $\{t_i\}$ ，并使用了一组算符 $\{f_i\}$ 来计算的。如果 $$z$$ 的每个子表达式都用一个整数来标记，则可以编写一个抽象程序来计算 $$z$$ ，方法是计算一个子表达式序列 $\langle y_i\rangle^n_{i = 1}$ ，并设置 $$z = y_n$$ 。算法5显示了这样一个程序。

每个终端表达式 $$t_i$$ 是程序的字面常量或输入参数。这包括了系数，基函数和几何量。一个非终端子表达式 $$y_i$$ 是将算符 $$f_i$$ 应用于先前计算过的表达式序列 $\langle y_j\rangle_{j\in \mathcal{J}_i}$ 的结果，其中 $\mathcal{J}_i$ 是表达式有序序列的记号。注意，根据已计算的子表达式，能产生的相同的 $$z$$ 值的顺序并不是唯一的。为了正确起见，我们只要求 $j\lt i\ \forall j\in\mathcal{J}_i$ ，这样子表达式 $$y_i$$ 的所有依赖关系都在 $$y_i$$ 之前计算出来了。特别是，在此抽象算法中，出于符号上的方便，所有终端表达式都最先编号。

计算z的程序可以表示成图，其中每个表达式 $$y_i$$ 对应于图顶点。如果 $j \in \mathcal{J}_i$ ，而 $$y_i$$ 依赖于 $$y_j$$ 的值，那么这是有向图的一个从 $$y_i$$ 到 $$y_j$$ 的边 $$e = (i, j)$$ 。更正式地讲，表示计算 $$z$$ 的图 $$G$$ 由一组顶点 $$V$$ 和一组边 $$E$$ 组成，它们由以下各项定义：

G = (V, E) \tag{17.65}

V = \langle v_i \rangle^n_{i=1} = \langle y_i \rangle^n_{i=1} \tag{17.66}

E = \{e_k\} =\bigcup^n_{i=1} \{(i, j)\ \forall j \in \mathcal{J}_i\} \tag{17.67}

此图明显是有向的，因为它的依赖关系是有向的。它是无环的，因为一个表达式只能根据现有的表达式构造。因此，UFL表达式可以用有向无环图（DAG）表示。在UFL中，此DAG可用两种方式表示。在定义表达式时，会建立一个称为表达式树的链表示。从技术上讲，这仍然是DAG，因为可以在多个子表达式中重用顶点，但是这个表示强调了DAG的树状结构。另一个表示称为计算图，它与上面 $$G$$ 的定义非常相似。此表示对形式编译器最有用。这两个DAG表示的细节将在下面说明。它们都将图形中顶点的表示作为表达式对象共享，下面将对其进行说明。

17·6·2 表达式对象

回顾一下算法5的非终端表达式 $y_i = f_i(\langle y_j \rangle_{j\in \mathcal{J}_i} )$ 。算符 $$f_i$$ 由表达式对象的类来表示，而表达式 $$y_i$$ 由此类的实例表示。在UFL实现中，每个表达式对象都是Expr的某个子类的实例。 Expr类是层次结构的超类，其中包含UFL所支持的所有终端表达式类型和算符类型。 Expr有两个直接的子类，Terminal和Operator，它们将表达式类型层次分为两部分，如图17.2所示。

图17.2 表达式类的层次结构。

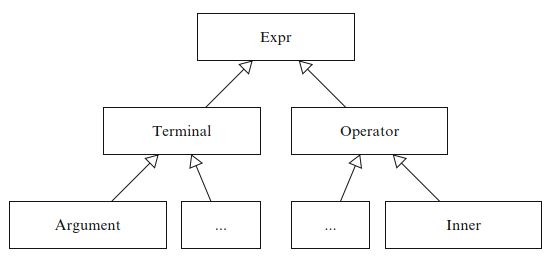
所有表达式对象都被认为是不可变的。一旦构造了表达式对象，将永远无法对其进行修改。操作表达式应始终会导致创建新对象。不可变属性确保表达式对象可以在表达式之间重用和共享，而不会在程序的其他部分产生副作用。这既减少了内存使用，避免了不必要的对象复制，又简化了对常见子表达式的识别。

在表示 $$y_i$$ 的Expr对象e上调用e.operands()，会返回一个具有表示 $\langle y_j \rangle_{j\in \mathcal{J}_i}$ 的表达式对象的元组。请注意，也可应用到没有传出边的终端表达式，并且t.operands()返回空元组。除了修改表达式对象的操作数外，还可以调用e.reconstruct(operands)用修改后的操作数构造相同类型的新表达式对象，其中operands是表达式对象元组。如果操作数相同，则此函数返回原始对象，从而允许许多算法节省内存而不会带来其他复杂性。不变式e.reconstruct(e.operands()) == e应该始终成立。

17·6·3 表达式属性

在第17.4.2节中，讨论了UFL的张量代数和索引记号的功能。表达式可以是标量或具有任意阶和形状的张量值。因此，每个表达式对象e的值形状为e.shape()，它是在每个张量轴上维数的整数元组。标量表达式也有shape ()。另一个重要的属性是表达式中的一组自由索引，可以使用e.free_indices()作为元组获得。尽管自由索引没有顺序，但为简单起见，它们以Index实例的元组表示。因此，元组中的排序没有任何意义。

UFL表达式在引用上是透明的，但有一些例外。 引用透明性是指子表达式可以用其值的另一种表示代替，而无需更改表达式的含义。这里的关键是，在这种情况下，表达式的值包括张量形状和一组自由索引。另一个重要点是，函数 $$f (v)$$ 在某点导数 $f'(v)|_{v=g}$ ，依赖于 $$v = g$$ 附近的函数值。这种依赖性的结果是，算符类型在微分时很重要，而不仅是微分变量的当前值。特别是，Variable不能用其表示的表达式替换，因为diff依赖于Variable实例，而不是有值的表达式。同样，用某个值替换Coefficient会更改包含关于函数系数求导表达式的含义。

以下示例说明了Variable和diff的这个问题。

# UFL code
e = 0
v = variable(e)
f = sin(v)
g = diff(f, v)

这里的 $$v$$ 是一个取值为0的变量，但是 $\sin(v)$ 不能简化为0，否则 $$f$$ 的导数将变成0。此处的正确结果是 $g = \cos(v)$ 。打印f和g得到字符串sin(var1(0))和d/d[var1(0)] (sin(var1(0)))。尝试仅设置 $$v = e$$ ，看看f和g如何变为零。

17·6·4 树表示

表达式树没有单独的数据结构。它只是查看表达式结构的一种方式。任何表达式对象e都可以看作是树的根，其中e.operands()返回其子级。如果某些子项相等，则它们的出现次数将与表达式中出现的次数相同。因此很容易遍历树节点（也就是DAG中的vi），但是最终无法直接重用子表达式。 DAG中的边不会明确显示，并且只能通过递归遍历树并选择唯一对象来获得顶点列表。

刚度项 $\mathrm{grad}\ u : \mathrm{grad}\ v$ 的表达式树如图17.3所示。终端表达式u和v没有子节点， $\mathrm{grad}\ u$ 项本身由带有两个节点的树表示。每次将算符应用于某些表达式时，它将返回引用其操作数的新树根。请注意，用户将在使用该语言时应用的是grad和inner函数，而该图中的名称Grad，Inner和Argument是UFL中用来表示表达式对象的Expr子类名称。换句话说，由grad(u) 获得的表达式梯度，是一个由Grad(u)表示的表达式，而inner(a, b)则给出一个表达式表示Inner(a, b)。语言和表示的这种分离仅仅是UFL实现中的一种设计选择。

图17.3

\mathrm{grad}\ u : \mathrm{grad}\ v

的表达式树。

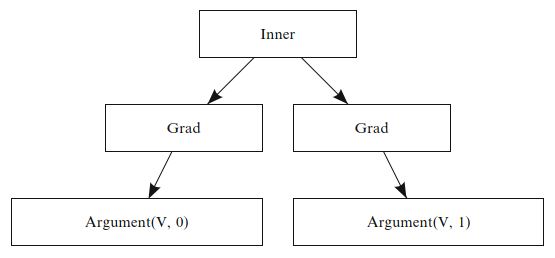
17·6·5 图表示

当以树的形式查看表达式时，所有唯一顶点和边的列表都不是直接可用的。更加直接地表示DAG可以简化或优化许多算法。 UFL包括从任何表达式构建基于DAG表示的数组的工具（计算图）。计算图 $$G = (V, E)$$ 是基于平面数组的数据结构，直接反映了方程（17.65）-（17.67）中图的定义。此表示可直接访问子表达式之间的依赖关系，并允许在唯一顶点上轻松进行迭代。该图可通过以下几行轻松构建：

# Python code
# from ufl.algorithms import Graph
from ufl.formatting.graph import Graph
G = Graph(expression)
V, E = G

一个数组（Python列表）V用于存储DAG中的顶点 $\langle v_i\rangle^n_{i=1}$ 。对于每个顶点 $$v_i$$ ，存储一个表达式节点 $$y_i$$ 来表示。因此，每个顶点的表达式树也是直接可用的，因为每个表达式节点都是其表达式树的根。边则存储在数组 $$E$$ 中，整数元组 $$(i,j)$$ 表示从 $$v_i$$ 到 $$v_j$$ 的边；也就是说， $$v_j$$ 是 $$v_i$$ 的操作数。图中的顶点列表是使用深度优先遍历的后序来构建的，这保证了对顶点进行拓扑排序，使得 $j\lt i\quad \forall j\in \mathcal{J}_i$ 。

让我们看一个计算图的例子。以下代码定义一个简单表达式，然后打印图的顶点和边缘。

# Python code
from ufl import *
cell = triangle
V = FiniteElement("Lagrange", cell, 1)
u = TrialFunction(V)
v = TestFunction(V)
c = Constant(cell)
f = Coefficient(V)
e = c*f**2*u*v

# from ufl.algorithms import Graph, partition
from ufl.formatting.graph import Graph, partition
G = Graph(e)
V, E, = G

print("str(e) = %s\n" % str(e))
print("\n".join("V[%d] = %s" % (i, v) for (i, v) in enumerate(V)), "\n")
print("\n".join("E[%d] = %s" % (i, e) for (i, e) in enumerate(E)), "\n")

程序输出的摘录如下所示：

# Generated code
V[0] = v_{-2}
...
V[7] = v_{-1} * c_0 * w_1 ** 2
V[8] = v_{-2} * v_{-1} * c_0 * w_1 ** 2
...
E[6] = (8, 0)
E[7] = (8, 7)

最后两个边，显示了顶点8与顶点7和0的依存关系，因为 $$v_8 = v_0 v_7$$ 。运行代码以查看该代码的完整输出。尝试更改表达式，然后如上查看图。

从边E可以有效地计算相关的数组。特别是顶点vi在两个方向上所依赖的顶点索引是有用的：

\begin{aligned}V_{out} &= \langle \mathcal{J}_i\rangle^n_{i=1} \\ V_{in} &= \langle \{j|i \in \mathcal{J}_j\}\rangle^n_{i=1}\end{aligned} \tag{17.68}

对任何表达式，这些数组可以很容易构造：

# Python code
Vin = G.Vin()
Vout = G.Vout()

存在类似的函数，用于获取所有传入和传出边E的索引。由UFL构建的计算图有一个不错的特性：没有两个顶点将代表完全相同的表达式。在图的构建期间，将子表达式插入哈希映射（Python字典）中即可实现此目的。一些表达式类对参数进行唯一排序，例如a*b和b*a将成为图中的相同顶点。

当实现某些算法时，表达式节点中的自由索引会使线性化图的解释复杂化，因为具有自由索引的表达式对象不代表一个值，而是代表一组值，自由索引的每个值排列都对应一个值。一种解决方案是在构造图之前应用expand_indices，它将用自由索引所对应的显式固定索引等效表达式，来替换所有表达式。但是请注意，展开无法重新获得自由索引。有关此转换的更多信息，请参见第17.8.3节。

17·6·6 划分

UFL旨在作为形式编译器的前端。由于最终目标是根据表达式生成代码，因此为代码生成过程提供了一些实用程序。原则上，只需在顶点上迭代并分别为每个操作生成代码，就可以从其计算图为表达式生成正确的代码，基本上是算法5的镜像。但是，一个好的形式编译器应该能够产生更好的代码。 UFL提供了实用程序，用于根据子表达式的依赖性将计算图划分为子图（划分），这允许基于形式编译器的正交，可以轻松地将子表达式放置在正确的循环集中。函数partition实现此功能。每个划分都由一个简单的顶点索引数组表示，并且每个划分都标记有一组依赖项。默认情况下，这组依赖使用字符串x，c和v%d来分别表示对空间坐标，特定数量的胞元和形式参数（非系数）的依赖关系。

以下示例代码对上面构建的图进行划分，并根据其依存关系将顶点分组打印。

# Python code
partitions, keys = partition(G)
for deps in sorted(partitions.keys()):
    P = partitions[deps]
    print("The following depends on", tuple(deps))
    for i in sorted(P):
        print("V[%d] = %s" % (i, V[i]))

该程序的输出文本见后。注意，字面常量2没有依赖。始终可以在编译时预先计算此划分中的表达式。常数c_0依赖于每个胞元的变化数据，由依赖集的c代表，而不依赖于空间坐标，因此可以将其置于正交循环之外。函数w_1及其依赖的表达式还依赖于x表示的空间坐标，因此需要针对每个正交点进行计算。仅依赖于测试或试探功能的表达式用v%d标记，其中数字是UFL用于区分参数的内部计数器。请注意，此处的测试和试探函数被标记所依赖的空间坐标，但是不依赖胞元的数量。这仅适用于在局部参考单元上定义的有限元，在这种情况下，可以在每个正交点中预先计算基函数。有限元空间中基本函数在运行时的实际依赖关系对于UFL是未知的，这就是为什么函数partition用可选的多功能参数，以便形式编译器可以提供更准确依赖关系的原因。有关此详细的实现信息，请参考partition的实现。

# Generated code
The following depends on ()
V[4] = 2
The following depends on ("c",)
V[2] = c_0
The following depends on ("x", "c")
V[3] = w_1
V[5] = w_1 ** 2
V[6] = c_0 * w_1 ** 2
The following depends on ("x", "v-1")
V[1] = v_{-1}
The following depends on ("x", "c", "v-1")
V[7] = v_{-1} * c_0 * w_1 ** 2
The following depends on ("x", "v-2")
V[0] = v_{-2}
The following depends on ("x", "c", "v-2", "v-1")
V[8] = v_{-2} * v_{-1} * c_0 * w_1 ** 2

【章节目录】