UFL:有限元形式语言》概述&有限元空间&形式【翻译】
【章节目录】
统一形式语言(UFL,Alnæs和Logg,2009年)是一种领域专用语言,用于描述变分形式和函数的有限元离散化。 更准确地说,该语言定义了一个灵活的用户接口,用于定义近似于数学符号弱形式的有限元空间和表达式。
FEniCS项目提供了一个框架,用于构建求解偏微分方程(PDE)的应用程序。 UFL是此框架的核心组件之一。 它定义了你表示PDE的语言。 它是形式编译器FFC和SFC的输入语言和前端,这在第11章和第15章中介绍过。 UFL实现还提供了可以用形式编译器简化编译过程的算法。 这些形式编译器的输出是符合UFC规范的C++代码(Stroustrup,1997),这在第16章中说明过。 该代码可与第10章介绍的C++/Python库DOLFIN一起使用,以有效地组装线性系统并计算PDE的解。 请注意,本章并未涵盖如何实际求解UFL中定义的方程。 有关如何使用完整的FEniCS框架求解方程式的教程,请参见第1章。
本章既适合希望学习如何表示方程式的FEniCS用户,也适合希望了解UFL在内部是如何工作的其他FEniCS开发人员和技术用户。 因此,本章的各节将组织更多的技术细节。 第17.1-17.5节概述了终端用户所看到的语言,并面向所有受众。 第17.6-17.9节解释了实现的设计,并深入一些实现细节。 在这样的行文中,必须省略该语言的许多细节,有关更详尽的描述,请参阅UFL手册(Alnæs和Logg,2009)。 请注意,本章涉及UFL版本1.0.0,并且用户接口和实现都可能在将来的版本中更改。
从简要概述开始,我们提及UFL的主要设计目标,并在第17.1节中展示非平凡PDE的实现例子。 接下来,我们将在第17.2节中介绍如何定义有限元空间,然后在第17.3节中介绍形式的整体结构及其描述。 该语言的主要部分涉及从一组数据类型和运算符定义表达式,这将在17.4节中讨论。 应用于形式整体的算符是第17.5节的主题。
本章的技术部分从第17.6节开始,讨论表达式的表示。 在这里定义的符号和数据结构基础上,第17.7节讨论了如何计算导数。 第17.8节讨论了一些核心内部算法及其实现中的关键问题。 第17.9节中的主题是一些特定编程语言Python(van Rossum等)中的实现细节。 最后,第17.10节讨论了UFL项目的未来前景。
17·0·1 相关工作
在其他几个项目中,也从其他角度追求:结合领域专用语言和符号计算的有限元方法。 Sundance(Long,2003,2004b,a)直接在C++中实现了一个符号引擎来定义变分形式,并支持自动微分。 Life项目(Prud’homme,2006b,a)使用基于表达模板技术的嵌入在C++的领域专用语言来指定变分形式。 SfePy(Cimrman等人,2008)使用SymPy作为符号引擎,并通过有限元方法对其进行了扩展。 GetDP(Dular和Geuzaine,2005年)是另一个使用领域专用语言表示变分形式的项目。 Mathematica软件包AceGen(Korelc,1997,2002)使用Mathematica的符号功能为有限元方法生成有效的代码。 所有这些软件包的共同点都集中在偏微分方程的高级描述上,以在仿真软件的开发中实现更高的人工效率。
UFL几乎类似于符号计算库,但其范围,目标和优先级与通用符号计算项目不同,例如GiNaC(Bauer等人,2002),Swiginac(Skavhaug和ˇCertík,2009)和SymPy(ˇCertík等人,2009)。 作为领域专用语言和形式编译器前端,UFL不适合大规模符号计算。
17·1 概述
17·1·1 设计目标
UFL是对FFC和SFC早期版本所使用形式语言的统一,完善和重新实现。 这种语言的发展受到诸多因素的推动,其中最重要的是:
- 一种更丰富的形式语言,尤其是其可用于表示非线性PDE。
- 表达式和形式的自动微分。
- 提高形式编译器技术的性能,来有效处理更复杂的方程。
UFL满足了所有这些要求,因此,它代表了FEniCS项目功能的重大进步。
FFC形式语言之后,支持张量代数和索引符号建模,并进一步推广。 该语言包括了一些以前仅SFC支持的非线性算符和函数。 表达式和形式的微分已成为该语言的一个组成部分,比以前在SFC中实现这些功能的方式要容易得多。 总之,UFL作为一种统一的形式语言,结合了FFC和SFC的优点,并增加了其他功能。
配合以前形式编译器基准,基于UFL的新一代形式编译器所生成的代码效率已被验证匹配。(Alnæs和Mardal,2010;Ølgaard和Wells,2010) 现在,形式编译过程足够快,可以融合到常规应用程序构建过程中。 以前需要太多内存来编译,或者花费数十分钟甚至几小时来编译的复杂形式,现在都可以在几秒钟内用SFC和FFC进行编译。
17·1·2 动机的例子
在UFL的最初开发过程中,一个主要的动机例子是具有大形变的弹性方程。 特别是,生物组织模型使用具有各向异性和强非线性的复杂超弹性本构定律。 为了用FEniCS实现这些方程,必须解决上面列出的所有三个设计目标。 下面显示了超弹性方程的一种形式及其对应的UFL实现。 请记住,这仅是为了说明形式语言和方程式自然表达之间的紧密对应关系。 这些方程的含义对于读者来说不是必需的。 第27章更详细地介绍了非线性弹性。 注意,许多其他示例与UFL一起分发。
在这里介绍的超弹性方程的公式中,未知函数是位移向量场 \(u\) 。 物性系数 \(c_1\) 和 \(c_2\) 是标量常数。 根据应变能量函数 \(W(C)\) ,计算第二类Piola-Kirchhoff应力张量 \(S\) 。 \(W\) 定义了本构定律,这里是简单的Mooney-Rivlin定律。 与位移和应力有关的方程式:
\[ \begin{aligned}F &= I + \mathrm{grad} \ u \\ C &= F^⊤ F \\ I_C &= \mathrm{tr}(C) \\ II_C &=\frac{1}{2}\left(\mathrm{tr}(C)^2 − \mathrm{tr}(CC)\right)\\ W &= c_1(I_C − 3) + c_2(II_C − 3)\\ S &= 2 \frac{\partial W} {\partial C} \end{aligned} \tag{17.1} \]为了简单起见,在此示例中,我们忽略了外部力和边界力,并假设为准稳态,从而导致以下力学问题。 寻求 \(u\) ,以满足:
\[ \mathrm{div}(FS) = 0, \qquad \mathrm{in} \ dx \tag{17.2} \] \[ u = u_0, \qquad \mathrm{on} \ ds \tag{17.3} \]有限元方法在第2章中介绍过,因此我们仅将简要地介绍此处采取的步骤。 首先,我们将等式(17.2)与测试函数 \(\phi\in V\) 相乘,然后在域 \(\Omega\) 上积分,然后分部积分。 于是,非线性变分问题读为:需求 \(u\in V\) ,满足
\[ L(u; \phi) = \int_\Omega FS : \mathrm{grad} \ \phi \ dx = 0 \qquad \forall \phi \in V \tag{17.4} \]为了简洁起见,这里我们省略了系数 \(c_1\) 和 \(c_2\) 。 将位移场近似为 \(u \approx u_h = \sum_k u_k \psi_k\) ,其中 \(\psi_k \in V_h \approx V\) 是试探函数,并使用牛顿法求解非线性方程,最终得到一个待求解的方程组
\[ \sum^{|V_h|}_{k=1}\frac{\partial L(u_h; \phi)}{\partial u_k} \Delta u_k = −L(u_h; \phi)\qquad \forall \phi \in V_h \tag{17.5} \]UFL可以自动计算与等式(17.5)左侧相对应的双线性形式 \(a(u; \psi, \phi)\) ,从而
\[ a(u_h; \psi_k, \phi) =\frac{\partial L(u_h; \phi)}{\partial u_k}\qquad k = 1,\dots, |V_h| \tag{17.6} \]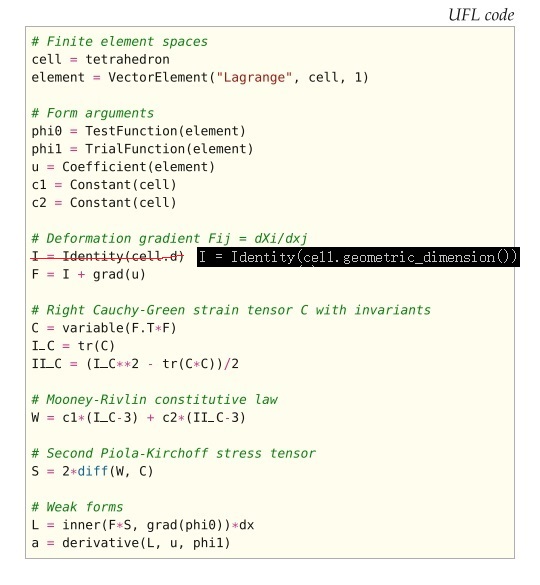
图17.1显示了UFL中公式(17.1),(17.4)和(17.6)的实现。 注意数学符号和UFL源代码之间的紧密关系。 特别要注意,本构定律和残差方程的自动微分。 算符diff可应用于表达式的微分(关于指定变量,例如C), 而算符derivative可以应用于整个形式的导数(关于比如 \(u\) 的离散函数的每个系数)。 这些特征的组合允许通过简单地改变 \(W\) 来实现新的物性定律,其余的则是自动的。 在以下各节中,将说明此实现中使用的符号,定义和算符。
17·2 定义有限元空间
多边形胞元在UFL中由基本形状定义,并被描述为
# UFL code
cell = Cell(shapestring)
UFL定义了一组有效的多边形胞元形状:“interval”,“triangle”,“tetrahedron”,“quadrilateral”和“hexahedron”。 所有形状的胞元对象都是预先定义的,可以用下面的写法代替
# UFL code
cell = tetrahedron
在本章的其余部分,变量名cell将被用于任何有合法参数胞元,以使示例的维数尽可能独立。
UFL定义了用于声明有限元空间的语法,但对实际的多项式基底或自由度一无所知的。 多项式基底是通过在预定的基本单元族中极其提供多项式次数来隐式选择的,但是UFL假定每个有限元空间 \(V_h\) 只存在一个具有固定顺序的基础; 那就是
\[ V_h = \mathrm{span} \left\{\phi_j\right\}^n_{j=1} \tag{17.7} \]基本的标量单元可以组合形成矢量单元或张量单元,并且单元可以轻松地组合为任意混合单元的层次结构。
UFL中的一组预定义单元族名称包括“ Lagrange”(简称“ CG”),代表标量Lagrange有限元(连续的分段多项式函数),“ Discontinuous Lagrange”(简称“ DG”),代表标量不连续的Lagrange有限元(不连续的分段多项式函数),以及可以在手册中找到的其他族的范围。 为了方便起见,每个族都有一个关联的简称。要从Python将所有有效族打印到屏幕,请调用show_elements()。
声明单元的语法最好通过一些示例进行解释。
# UFL code
cell = tetrahedron
P = FiniteElement("Lagrange", cell, 1)
V = VectorElement("Lagrange", cell, 2)
T = TensorElement("DG", cell, 0, symmetry=True)
TH = V*P
ME = MixedElement(T, V, P)
在第一行中,从一组预定义的胞元中选择一个多边形胞元。 然后声明了标量线性拉格朗日单元P,以及二次矢量拉格朗日单元V。 接下来定义一个对称的2秩张量单元T,它在每个胞元上也是分段恒定的。 代码继续声明了混合单元TH,该单元将二次矢量单元V和线性标量单元P组合在一起。 该单元被称为Taylor-Hood单元。 最后,声明另一个具有三个子单元的混合单元。 请注意,T*V*P的写法不会导致具有三个直接子单元的混合单元,而只会产生MixedElement(MixedElement(T, V), P)。
17·3 定义形式
考虑在 \(\partial\Omega_0\) 和 \(\partial\Omega_1\) 上两个不同边界条件的泊松方程,
\[ a(w; u, v) = \int_\Omega w \ \mathrm{grad} \ u \cdot \mathrm{grad} \ v \ dx \tag{17.8} \] \[ L(f , g, h; v) = \int_\Omega f v \ dx + \int_{\partial \Omega_0}g^2 v \ ds + \int_{\partial \Omega_1}h v \ ds \tag{17.9} \]这些形式可以在UFL中表示为:
# UFL code
a = w*dot(grad(u), grad(v))*dx
L = f*v*dx + g**2*v*ds(0) + h*v*ds(1)
其中,乘以测度dx,ds(0)和ds(1)分别表示积分 \(\int_{\Omega}(\cdot)dx\) ,积分 \(\int_{\Omega_0}(\cdot)ds\) 和 \(\int_{\Omega_1}(\cdot)ds\) 。
UFL所表示的形式用于有限元离散化,然后编译为用于计算单元张量的有效代码。 考虑上面的示例,在一系列基函数并且系数函数固定后,具有一个系数函数 \(w\) 的双线性形式 \(a\) 在各点已被算出,即
\[ V_h^1 = \mathrm{span} \left\{\phi_k^1\right\}, V_h^2 = \mathrm{span} \left\{\phi_k^2\right\}, V_h^3 = \mathrm{span} \left\{\phi_k^3\right\} \tag{17.10} \] \[ w =\sum^{|V_h^3|}_{k=1}w_k\phi_k^3, \qquad \{w_k\} 给定 \tag{17.11} \] \[ A_{ij} = a(w; \phi_i^1, \phi_j^2), \qquad i = 1, \cdots, |V_h^1|, j = 1,\cdots , |V_h^2| \tag{17.12} \]通常,UFL旨在表示以下一般化的形式:
\[ \begin{aligned}&a(w^1, . . . , w^n; \phi^1, \dots, \phi^r) \\ = &\sum^{n_c}_{k=1} \int_{\Omega_k}I_k^c dx + \sum^{n_e}_{k=1} \int_{\partial\Omega_k}I_k^e ds + \sum^{n_i}_{k=1} \int_{\Gamma_k}I_k^i dS \end{aligned}\tag{17.13} \]本章的大部分内容讨论定义积分表达式 \(I_k^c\) , \(I_k^e\) 和 \(I_k^i\) 的方法。 其余的符号将在下面说明。
形式的参数分为两组,即基函数 \(\phi^1, \dots , \phi^r\) 和系数函数 \(w^1, \dots , w^n\) 。 所有 \(\{\phi^k\}\) 和 \(\{w^k\}\) 都是具有一个基底的某些离散函数空间中的函数。 注意,UFL从来不知道具体的基函数 \(\{\phi_j^k\}\) 和系数 \(\{w_k\}\) ,但是我们假设每个有限元空间的基底都是固定的。 固定顺序仅在要区别不同形式时才重要,如第17.7节所述。
有效形式表达式的每个项都必须是一个精确积分的标量值表达式,并且在 \(\{\phi^k\}\) 中必须是线性的。 任何项都可能对系数函数具有非线性依赖。 带有一个或两个基函数参数(r = 1, 2)的形式分别称为线性形式或双线性形式,而忽略了它对系数函数的依赖。 在应用程序中使用时,它们将被组装成向量和矩阵。 仅依赖系数函数(r = 0)的形式称为泛函,因为它将被组装为实数。 r>2的多重线性形式也被支持,但不常用的。
整个域表示为 \(\Omega\) ,外部边界表示为 \(\partial \Omega\) ,而三角剖分的一组内部维面表示为 \(\Gamma\) 。 子域用一个后缀标记,例如 \(\Omega_k\subset\Omega\) 。 如上所述,积分是通过与测度相乘来表示的,并且UFL定义了测度 \(dx\) , \(ds\) 和 \(dS\) 。 总之,存在三种具有相应UFL表示形式的积分
- \(\int_{\Omega_k}(\cdot)dx \leftrightarrow (\cdot)*dx(k)\) ,称之为胞元积分,
- \(\int_{\partial\Omega_k}(\cdot)ds \leftrightarrow (\cdot)*ds(k)\) ,称之为外维面积分,
- \(\int_{\Gamma_k}(\cdot)dS \leftrightarrow (\cdot)*dS(k)\) ,称之为内维面积分。
可以通过将元数据附加到测度对象上来实现为形式的每项定义不同的正交顺序,例如
# UFL code
dx02 = dx(0, { "integration_order": 2 })
dx14 = dx(1, { "integration_order": 4 })
dx12 = dx(1, { "integration_order": 2 })
L = f*v*dx02 + g*v*dx14 + h*v*dx12
元数据还可用于为每项分别覆盖其他形式编译器特定选项。 有关此特性的更多详细信息,请参见UFL和形式编译器的手册。
【章节目录】