DOLFIN：C++/Python有限元库》注记【翻译】

2021-01-13

| 科学计算 | | FEniCS , 有限元法 , 偏微分方程 | 评论

【章节目录】

10·4 实现注记

在本节中，我们讨论DOLFIN实现的特定方面，包括并行计算，Python接口的生成，以及即时编译。

10·4·1 并行计算

DOLFIN支持从多核工作站到大规模的并行超级计算机的并行计算。 它的设计，使用户可以用与串行计算相同的代码来执行并行仿真。

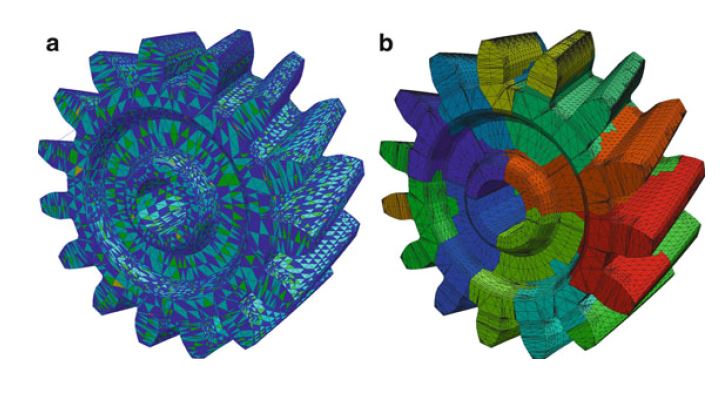
支持两种并行仿真范式。 第一个范式是共享机器内存的多线程。 第二个范式是针对分布式存储器的完全分布式并行化。 对于这两种范式，都需要对网格进行特殊的预处理。 对于多线程并行化，使用了所谓的着色方法（请参见图10.8a），对于分布式并行化，使用了网格划分方法（请参见图10.8b）。 下面讨论这两种方法的各个方面。 也可以将这些方法组合在一起，从而产生混合方法，以利用现代多核处理器集群的功能。

共享内存并行计算。 使用OpenMP支持在共享内存机器上对有限元矩阵和向量进行多线程组装。 通过参数系统，设置要使用的线程数来激活它。 例如，代码

// C++ code
parameters["num_threads"] = 6;

指示DOLFIN在组装过程中使用六个线程。 在组装期间，DOLFIN在网格中的胞元或胞元维面上循环，并计算对全局矩阵或向量的局部贡献，然后将其添加到全局矩阵或向量中。 使用多线程组装时，将为每个线程分配所负责的胞元或维面集。 这对用户是透明的。

多线程的使用，要求设计时注意避免出现竞争状况（多个线程试图同时写入同一内存位置）。 竞争状况通常会导致程序的行为无法预测。 为了避免在组装过程中出现竞争状况（如果两个线程几乎同时将值添加到全局矩阵或向量中），DOLFIN使用图形着色方法。 在组装之前，对给定进程中的网格“着色”，以便为每个胞元分配一种颜色（实际上是整数），以满足，没有两个相邻的胞元具有相同的颜色。 对于给定问题，胞元是相邻的意义取决于所用有限元的类型。 在大多数情况下，共享顶点的胞元被认为是邻居，但是在其他情况下，共享边或维面的胞元也可能被认为是邻居。 在组装过程中，按颜色组装胞元。 所有第一种颜色的胞元在线程之间共享并组装，然后是下一种颜色。 由于相同颜色的胞元是不相邻的，因此不共享全局矩阵或向量中的实体，因此在组装过程中不会发生竞争状况。 LFIN中的网格着色，使用了Boost Graph Library接口或Zoltan接口（属于Trilinos项目的一部分）。 图10.8a显示了已着色的网格，使得没有两个相邻的胞元（在共享维面的意义上）具有相同的颜色。

第三方线性代数库中多线程的支持，目前受限的，但这是一个活跃的领域。 可以通过PETSc线性代数后端，来访问支持多线程并发的LU求解器PaStiX。

分布式内存并行计算。 使用消息传递接口（MPI）支持完全分布式并行计算。 为了能执行并行仿真，应该在MPI和启用了并行线性代数后端（例如PETSc或Trilinos）的情况下编译DOLFIN。 要运行并行仿真，应使用mpirun启动DOLFIN程序（要启动的MPI的程序名，在某些计算机上可能有所不同）。 使用16个进程的C++程序，可使用以下命令执行：

# Bash code
mpirun -n 16 ./myprogram

and for Python:

# Bash code
mpirun -n 16 python myprogram.py

DOLFIN支持完全分布式的并行网格，这意味着每个处理器仅拥有其所负责的网格部分副本。 这种方法是可扩展的，因为不需要处理器来保存完整网格的副本。 并行仿真中的一个重要步骤是网格划分。 DOLFIN可以使用ParMETIS和SCOTCH（Pellegrini）库并行执行网格划分。 可以通过参数系统指定用于网格划分的库，例如，使用SCOTCH：

// C++ code
parameters["mesh_partitioner"] = "SCOTCH";

或使用ParMETIS：

# Python code
parameters["mesh_partitioner"] = "ParMETIS"

图10.8b显示了已被并行划分为12个域的网格。 每个域都由一个进程负责。

如果使用MPI启动并行程序，并启用了并行线性代数后端，那么线性代数运算将被并行执行。 在大多数应用程序中，这对用户是透明的。 PVD输出格式支持用于后处理的并行输出，并且其使用方式与串行输出相同。 每个进程都写入一个输出文件，并且单个主输出文件指向由不同进程产生的文件。

10·4·2 实现和Python接口生成

DOLFIN C++库，通过简单的包装程序和接口生成器SWIG（Beazley，1996； SWIG），为Python提供了封装； 有关更多详细信息，请参见第19章。 封装后的C++库，可通过DOLFIN主dolfin模块内名为cpp的Python模块来访问。【译者注：大部分情况下，可直接访问对应的类/函数名，而无须戴上包含cpp.的类路径】 这意味着可以通过以下方式直接访问其已编译模块的所有功能和类的：

# Python code
from dolfin import cpp
Function = cpp.function.Function #  原文是： cpp.Function
assemble = cpp.fem.assemble # 原文是：cpp.assemble

cpp模块中的类和函数与C++接口中的相应类和函数具有相同的功能。 除了由SWIG自动生成的包装层之外，DOLFIN Python接口还依赖于直接在Python中实现的许多组件。 两者都被导入到名为dolfin的Python模块中。 在以下各节中，介绍了有助于这种集成的DOLFIN接口关键自定义项。 Python接口还与NumPy和SciPy工具包很好地集成在一起，这也在下面讨论。

10·4·3 UFL集成和即时编译器

在Python接口中，UFL形式语言已与Python封装的DOLFIN C++模块集成在一起。 在解释集成时，我们在本节中使用符号dolfin::Foo或dolfin::bar来表示DOLFIN中的C++类或函数。 对应的SWIG包装类或函数将记作cpp.Foo和cpp.bar。 UFL中的类将记为ufl.Foo，而UFC中的类将记为ufc::foo（注意小写）。 C++封装库顶部附加的Python层中，Python类和函数将记为dolfin.Foo或dolfin.bar。 为方便起见，有时会跳过类和函数的前缀。 本节中介绍的大多数代码段都是伪代码。 其目的是说明特定方法或功能的逻辑。 可能会故意排除部分实际代码。 有兴趣的读者可以检查代码中的特定类或函数，以全面了解实现。

函数空间的构造。 在Python接口中，集成了ufl.FiniteElement和dolfin::FunctionSpace。 FunctionSpace的声明与ufl.FiniteElement的声明类似，但是FunctionSpace构造函数使用cpp.Mesh（dolfin.Mesh）代替胞元类型（例如，三角形）：

# Python code
mesh = UnitSquare(8, 8)
V = FunctionSpace(mesh, "Lagrange", 1)

在FunctionSpace的Python构造函数中，ufl.FiniteElement的实例化。 FiniteElement被传递给即时（JIT）编译器，该编译器返回已编译且Python封装的ufc对象：ufc::finite_element和ufc::dofmap。 这两个对象，与网格一起，用于实例化cpp.FunctionSpace。 以下伪代码说明了从Python接口实例化FunctionSpace的方法：

# Python code
class FunctionSpace(cpp.FunctionSpace):
    def __init__(self, mesh, family, degree):
        # Figure out the domain from the mesh topology
        if mesh.topology().dim() == 2:
            domain = ufl.triangle
        else:
            domain = ufl.tetrahedron

        # Create the UFL FiniteElement
        self.ufl_element = ufl.FiniteElement(family, domain, degree)

        # JIT compile and instantiate the UFC classes
        ufc_element, ufc_dofmap = jit(self.ufl_element)

        # Instantiate DOLFIN classes and finally the FunctionSpace
        dolfin_element = cpp.FiniteElement(ufc_element)
        dolfin_dofmap = cpp.DofMap(ufc_dofmap, mesh)
        cpp.FunctionSpace.__init__(self, mesh, dolfin_element, dolfin_dofmap)

构造参数（试探和测试函数）。 ufl.Argument类（ufl.TrialFunction和ufl.TestFunction的基类）是Python接口的子类。 作为使用ufl.FiniteElement类实例化的替代，可使用DOLFIN FunctionSpace：

# Python code
u = TrialFunction(V)
v = TestFunction(V)

通过从所传递的FunctionSpace中提取ufl.FiniteElement，来在子类构造函数中实例化ufl.Argument基类，以下伪代码对此进行了说明：

# Python code
class Argument(ufl.Argument):
    def __init__(self, V, index=None):
        ufl.Argument.__init__(self, V.ufl_element, index)
        self.V = V

然后使用子类Argument来定义TrialFunction和TestFunction：

# Python code
def TrialFunction(V):
    return Argument(V, -1)

def TestFunction(V):
    return Argument(V, -2)

系数，函数和表达式。 使用Coefficient定义UFL形式时，用户在组装形式之前必须将其与离散有限元Function或用户定义的Expression相关联。 在DOLFIN C++接口中，用户需要显式地执行此关联（L.f = f）。 在DOLFIN Python接口中，ufl.Coefficient类与DOLFIN Function和Expression类组合，并且形式表达式（Coefficient）中的符号系数及其值（Function或Expression）之间的关联是自动的。 因此，用户可以直接组装，由这些组合类实例来定义的形式：

# Python code

class Source(Expression):
    def eval(self, values, x):
        values[0] = sin(x[0])

v = TestFunction(V)
f = Source()
L = f*v*dx
b = assemble(L)

Python接口中的Function类是从ufl.Coefficient和cpp.Function继承的，如以下伪代码所示：

# Python code
class Function(ufl.Coefficient, cpp.Function):
    def __init__(self, V):
        ufl.Coefficient.__init__(self, V.ufl_element)
        cpp.Function().__init__(self, V)

实际的构造函数还包括从其他对象实例化Function的逻辑。实际的构造函数还包括从其他对象实例化Function的逻辑。 关于对子函数的访问处理，还包括更复杂的逻辑。

可以通过两种不同的方式来创建用户定义表达式：（i）作为纯Python表达式； 或（ii）作为JIT编译表达式。 纯Python表达式是从Python中Expression子类实例化的对象。【译者注：在较新的版本中，用户定义表达式继承自UserExpression】 上面的Source类就是一个例子。 Expression类的构造函数的伪代码类似于Function类的伪代码：

# Python code
class Expression(ufl.Coefficient, cpp.Expression):
    def __init__(self, element=None):
        if element is None:
            element = auto_select_element(self.value_shape())
        ufl.Coefficient.__init__(self, element)
        cpp.Expression(element.value_shape())

如果用户未定义ufl.FiniteElement，DOLFIN将使用auto_select_element函数自动选择一个单元。 此函数将携带Expression的一个“值形状”，作为参数。 用户必须通过重载value_shape方法为向量值或张量值的表达式提供此属性。 基类cpp.Expression使用ufl.FiniteElement的"值形状"来进行初始化。

实际的代码比上面展示的要复杂得多，作为同一个类，Expression同时被用于处理JIT编译的和纯Python表达式。 还要注意，实际的子类最终是由Python中的元类生成的，这使得可以为已声明的子类作诸如完整性检查。

在SWIG生成的C++层中，cpp.Expression类由所谓的导子（director）类来封装。 这意味着整个Python类都由dolfin::Expression的C++子类封装的。 C++基类的每个虚拟方法都由SWIG在C++中生成的子类实现。C++基类的每个虚拟方法都由SWIG在C++中生成的子类实现。 这些方法调用该方法的Python版本，用户最终通过在Python中cpp.Expression的子类来实现该方法。

即时编译表达式。 每次表达式求值时都会从C++回调到Python，因此纯Python表达式的性能可能不太理想。 为了避免这种情况，用户可以使用JIT编译的Expression来替代C++版本的Expression的子类。 因为子类是用C++实现的，所以它不会涉及到Python的任何回调，因此比纯Python表达式要快得多。 通过将C++代码字符串传递给Expression构造函数来生成JIT编译的Expression：

# Python code
e = Expression("sin(x[0])")

所传递的字符串用于在C++中生成dolfin::Expression的子类，在该子类中内联到重载的eval方法中。 最终代码是由JIT编译，并使用Instant打包到Python的（请参见第14章）。 然后将生成的Python类导入Python。 该类尚未实例化，因为最终的JIT编译的Expression还需要从ufl.Coefficient继承。 为此，我们动态创建一个类，该类同时从生成的类和ufl.Coefficient继承。

可以使用类型函数在运行时创建Python中的类。 创建类并返回该类的实例的逻辑在dolfin.Expression的__new__方法中处理，如以下伪代码所示：

# Python code
class Expression(object):
    def __new__(cls, cppcode=None):
        if cls.__name__ != "Expression":
            return object.__new__(cls)
        cpp_base = compile_expressions(cppcode)
    def __init__(self, cppcode):
        ...
        generated_class = type("CompiledExpression",
                              (Expression, ufl.Coefficient, cpp_base),
                              {"__init__": __init__})
        return generated_class()

实例化JIT编译的Expression时，将调用__new__方法。 但是，当在基类的初始化过程中实例化Expression纯Python子类时，也会调用它。 我们通过检查实例化类名来处理两种情况。 如果该类的名称不是“Expression”，则该调用源自Expression的子类的实例化。 当实例化一个纯Python表达式时，如上面的代码示例中的Source实例，将调用object的__new__方法并返回实例化的对象。 在另一种情况下，当实例化JIT编译表达式时，如上所述，我们需要根据所传递的Python字符串来生成JIT编译基类。 这可以通过调用compile_expressions函数来完成。 在调用type生成最终类之前，先为该类定义__init__方法。 此方法通过自动选择单元类型，并为所创建的Expression设置尺寸来启动新对象。 此过程类似于对Python的Expression类派生。 最后，我们构造一个新类，该类通过调用type来继承JIT编译类和ufl.Coefficient。

type函数有三个参数：类名（“CompiledExpression”），基类（Expression，ufl.Coefficient，cpp_base）以及用于定义类的接口（方法和属性）的字典。 我们提供给生成类的唯一新方法或属性是__init__方法。 生成类后，我们将其实例化并将对象返回给用户。

UFL形式的组装。 DOLFIN Python接口中的assemble函数，运行用户可以直接组装已声明的UFL形式：

# Python code
mesh = UnitSquare(8, 8)
V = FunctionSpace(mesh, "Lagrange", 1)
u = TrialFunction(V)
v = TestFunction(V)
c = Expression("sin(x[0])")
a = c*dot(grad(u), grad(v))*dx
A = assemble(a)

assemble函数是包装自cpp.assemble函数浅层封装包。 以下伪代码说明了在此层所发生的情况：

# Python code
def assemble(form, tensor=None, mesh=None):
    dolfin_form = Form(form)
    if tensor is None:
        tensor = create_tensor(dolfin_form.rank())
    if mesh is not None:
        dolfin_form.set_mesh(mesh)
    cpp.assemble(dolfin_form, tensor)
    return tensor

此处，form是一个ufl.Form，用于生成dolfin.Form，如下所述。 除了form参数，用户可以选择提供张量和（或）网格。 如果未提供张量，则create_tensor函数将自动生成一个张量。 如果form不包含任何参数或函数，那么mesh是可选的。 例如，当组装汇仅包含表达式的函数时。 请注意，以上签名的长度已缩短。 assemble函数还有其他参数，但为清楚起见，此处将其忽略。

以下伪代码演示了dolfin.Form的构造函数中发生的情况，该构造函数从ufl.Form初始化了基类cpp.Form：

# Python code
class Form(cpp.Form):
    def __init__(self, form):
        compiled_form, form_data = jit(form)
        function_spaces = extract_function_spaces(form_data)
        coefficients = extract_coefficients(form_data)
        cpp.Form.__init__(self, compiled_form, function_spaces, coefficients)

form首先被传给dolfin.jit函数，用来调用已注册的形式编译器，生成代码，然后JIT对其进行编译。 当前可以选择两种形式的编译器：“ffc"和"sfc”（参见第11章和第15章）。 每种形式编译器中都定义自己的jit函数，该函数最终将接收该调用。 可以通过设置来选择形式编译器：

# Python code
parameters["form_compiler"]["name"] = "sfc"

默认的形式编译器是"ffc"。 形式编译器的jit函数返回JIT已编译的ufc::form以及ufl.FormData对象。 后者是一个包含ufl.form元数据的数据结构，用于提取实例化cpp.Form所需的函数空间和系数。 这些数据的提取由extract_function_spaces和extract_coefficients函数处理。

10·4·4 NumPy和SciPy整合

DOLFIN Python接口中的Matrix和Vector类的值可视为NumPy数组。 这是通过调用向量或矩阵的数组方法来完成的：

# Python code
A = assemble(a)
AA = A.array()

在此，A是从形式a组装而来的矩阵。 NumPy数组AA是稠密结构，并且所有值都是从原始数据中复制的。 array函数可以在分布式矩阵或向量上调用，在这种情况下，它将返回存储于本地值。

直接访问线性代数数据。 uBLAS和MTL4线性代数后端可以直接访问底层数据。uBLAS和MTL4线性代数后端可以直接访问底层数据。 通过data方法，返回作为数据视图的NumPy数组：

# Python code
parameters["linear_algebra_backend"] = "uBLAS"
b = assemble(L)
bb = b.data()

此处，b是uBLAS向量，bb是数据b的NumPy视图。 对bb的任何更改将直接影响b。 矩阵也存在类似的方法：

# Python code
parameters["linear_algebra_backend"] = "MTL4"
A = assemble(a)
rows, columns, values = A.data()

从压缩行存储格式返回的数据，三个NumPy数组：rows，columns和values。 这些也是代表A的数据视图。 values的任何变化都将直接导致A的相应变化。

稀疏矩阵和SciPy集成。 rows，columns和values的数据结构可用于从scipy.sparse模块实例化一个csr_matrix（Jones et al。，2009）：

# Python code
from scipy.sparse import csr_matrix
rows, columns, values = A.data()
csr = csr_matrix((values, columns, rows))

然后，可以将csr_matrix与其他支持稀疏矩阵的Python模块一起使用，例如scipy.sparse模块和pyamg，后者是代数多网格求解器（Bell等，2011）。

向量切片。 NumPy为NumPy数组提供了方便的切片接口。 DOLFIN Python接口也提供了向量接口（有关实现的详细信息，请参见第19章）。 切片可用于访问和设置向量中的数据：

# Python code

# Create copy of vector
b_copy = b[:]

# Slice assignment (c can be a scalar, a DOLFIN vector or a NumPy array)
b[:] = c

# Set negative values to zero
b[b < 0] = 0

# Extract every second value
b2 = b[::2]

NumPy切片与DOLFIN向量切片之间的区别在于NumPy数组的切片可提供对原始数组的视图，而DOLFIN中提供的是副本。 整数列表/元组，或NumPy数组也可以用于访问和设置向量中的数据。

# Python code
b1 = b[[0, 4, 7, 10]]
b2 = b[array((0, 4, 7, 10))]

10·5 历史注记

DOLFIN的第一个公开版本是0.2.0版，于2002年发布。 那时，DOLFIN是一个独立的C++库，具有最小的外部依赖性。 然后，所有功能都作为DOLFIN本身的一部分实现，包括线性代数和有限元形式求值。 尽管仅支持分段线性单元，但DOLFIN提供了变分形式的基本自动化有限元组件。 形式语言是由C++操作符重载实现的。 有关FEniCS形式语言开发概述，以及DOLFIN中实现的早期形式语言的示例，请参见第11章。

后来，DOLFIN的部分功能已移至外部库或其他FEniCS组件。 FEniCS项目于2003年诞生，此后不久，即2004年发布了0.5.0版本，DOLFIN中的形式求值系统被基于FFC和FIAT的自动代码生成系统所取代。 在第二年，线性代数被PETSc数据结构和求解器的包装器所取代。 这时，引入了DOLFIN Python接口（PyDOLFIN）。 从那时起，Python接口已经从用于DOLFIN C++功能的简单的自动生成的包装层发展到成熟的问题解决环境，该环境支持即时编译变分形式并与外部Python模块（例如NumPy）集成。

在2006年，简化并重新实现了DOLFIN网格数据结构，以提高效率并扩展功能。 新的数据结构是基于一个轻量级面向对象层，其位于普通连续C/C++数组的底层数据存储之上的，并且与基于完全对象的旧实现相比，效率提高了几个数量级。 本地存储所有网格实体（如胞元和顶点）的面向对象的实现。 带有新网格库的DOLFIN第一个版本是0.6.2版。

在2007年，引入了UFC接口，并将FFC形式语言与DOLFIN Python接口集成在一起。 还引入了即时编译。 第二年，对DOLFIN的线性代数接口进行了重新设计，从而可以灵活地处理多个线性代数后端。 2009年，在DOLFIN中引入并行计算时，达到了一个重要的里程碑。

多年来，DOLFIN对设计，接口和实现进行了许多更改。 但是，自从DOLFIN 0.9.0发布以来，它基于新的函数空间抽象引入了DOLFIN函数类的重新设计，仅对接口进行了较小的更改。 自0.9.0版发布以来，在预期第一个稳定版本DOLFIN 1.0版中，完善接口，实现缺少的功能，修复错误和改进文档的大多数工作都已完成。

【章节目录】