有限元变分形式的张量表示【翻译】

2021-01-05

| 科学计算 | | FEniCS , 有限元法 , 偏微分方程 |

在第6章中，对有限元变分问题离散化，我们看到在矩阵和向量组装中的一个重要步骤是计算由下式定义的胞元（单元）张量 $$A_T$$

A_{T,i} = a_T(\phi_{i_\rho}^{T,\rho}, \dots , \phi_{i_2}^{T,2}, \phi_{i_1}^{T,1}) \tag{8.1}

这里， $$a_T$$ 是对多重线性形式 $a:V_\rho\times\dots\times V_2\times V_1 \to \mathbb{R}$ 的局部贡献， $i=(i_1,i_2,\dots,i_\rho)$ 是长为 $\rho$ 的多重指标，并且 $\{\phi_k^{T,j}\}^{n_j}_{k=1}$ 是局部胞元 $$T$$ 上的局部有限元空间 $V_{j,h} \subset V_j,\quad j = 1, 2, \dots, \rho$ 的基底。在本章中，我们描述了如何通过称为张量表示的方法来有效地计算胞元张量 $$A_T$$ 。

8·1 泊松方程的张量表示

我们首先描述如何将泊松方程的胞元张量表达为一种特殊的张量缩并，并在下面解释如何将其推广到其他变分形式。对泊松方程，胞元张量（矩阵） $$A_T$$ 定义如下

A_{T,i} = \int_T \nabla\phi_{i_1}^{T,1} \cdot \nabla\phi_{i_2}^{T,2} dx = \int_T \sum^d_{\beta=1}\frac{\partial \phi_{i_1}^{T,1}}{\partial x_\beta}\frac{\partial \phi_{i_2}^{T,2}}{\partial x_\beta}dx \tag{8.2}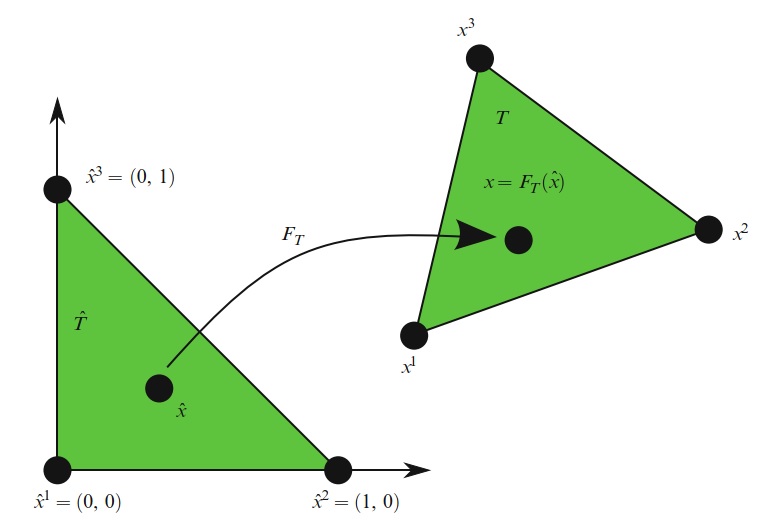

图8.1 从参考胞元

\hat{T}

到胞元

T \in \mathcal{T}_h

的（仿射）映射

\(F_T\)

。

令 $F_T:\hat{T}\to T$ 是从参考胞元 $\hat{T}$ 到当前胞元 $$T$$ 的仿射映射，如图8.1所示。使用这个仿射映射，我们作变量变化

A_{T,i} = \int_{\hat{T}}\sum^d_{\beta=1}\sum^d_{\alpha_1=1}\frac{\partial \hat{x}_{\alpha_1}}{\partial x_\beta}\frac{\partial \hat{\phi}_{i_1}^1}{\partial \hat{x}_{\alpha_1}}\sum^d_{\alpha_2=1}\frac{\partial \hat{x}_{\alpha_2}}{\partial x_\beta}\frac{\partial \hat{\phi}_{i_2}^2}{\partial \hat{x}_{\alpha_2}}\mathrm{det} \ F'_T d\hat{x} \tag{8.3}

在此， $\hat{\phi}_i^j = \phi_i^{T,j} \circ F_T$ 表示与当前胞元 $$T$$ 上的基函数 $\phi_i^{T,j}$ 相对应的参考胞元 $\hat{T}$ 上的基函数。由于 $$F_T$$ 是仿射的，因此偏导数 $\partial \hat{x}/\partial x$ 和行列式 $\mathrm{det} \ F'_T$ 都是常量的。因此，我们有

\begin{aligned}A_{T,i} &= \mathrm{det} \ F'_T \sum^d_{\alpha_1=1}\sum^d_{\alpha_2=1}\sum^d_{\beta=1}\frac{\partial \hat{x}_{\alpha_1}}{\partial x_\beta}\frac{\partial \hat{x}_{\alpha_2}}{\partial x_\beta}\int_{\hat{T}}\frac{\partial \hat{\phi}_{i_1}^1}{\partial \hat{x}_{\alpha_1}}\frac{\partial \hat{\phi}_{i_2}^2}{\partial \hat{x}_{\alpha_2}}d\hat{x} \\ &= \sum^d_{\alpha_1=1}\sum^d_{\alpha_2=1} A^0_{i\alpha} G^\alpha_T \end{aligned} \tag{8.4}

其中

\begin{aligned} A^0_{i\alpha} &= \int_{\hat{T}}\frac{\partial \hat{\phi}_{i_1}^1}{\partial \hat{x}_{\alpha_1}}\frac{\partial \hat{\phi}_{i_2}^2}{\partial \hat{x}_{\alpha_2}}d\hat{x} \\ G^\alpha_T &= \mathrm{det} \ F'_T \sum^d_{\beta=1}\frac{\partial \hat{x}_{\alpha_1}}{\partial x_\beta}\frac{\partial \hat{x}_{\alpha_2}}{\partial x_\beta} \end{aligned}\tag{8.5}

我们将张量 $$A^0$$ 称为参考张量，将张量 $$G_T$$ 称为几何张量。因此，我们可以将泊松方程胞元张量 $$A_T$$ 的计算表示为张量缩并

A_T = A^0 : G_T \tag{8.6}

可以通过预先计算参考张量 $$A^0$$ 的项来高效计算张量缩并。这是可能做到的，因为参考张量是常量的，并且不依赖于胞元 $$T$$ 或网格 $\mathcal{T}_h = \{T\}$ 。因此，在每个胞元 $T\in \mathcal{T}_h$ 上，可以通过首先计算几何张量 $$G_T$$ ，然后将其与预先计算的参考张量进行缩并来计算胞元张量。在第11章中，我们描述了FEniCS形式编译器（FFC），它在编译时预先计算参考张量 $$A^0$$ 并生成用于计算张量缩并的代码。

对二维泊松方程，张量缩并涉及将2×2几何张量GT与3×3×2×2参考张量 $$A^0$$ 的每个对应块缩并，以形成3×3胞元张量 $$A_T$$ 的项。因此，可以仅在四个乘-加对中计算各项（加上计算几何张量的成本）。与通过运行时正交计算相比，这带来了可观的提速，尤其是对于高次单元。在第9章中，我们讨论了如何通过检查参考张量A0的结构以发现张量缩并的简化算法来进一步改善这一点。

8·2 表示定理

在Kirby和Logg（2006）中，证明了任何仿射映射的单项式多重线性形式的胞元张量都可以表示为张量缩并之和：

A_T = \sum_k A^{0,k} : G_{T,k} \tag{8.7}

单项式多重线性形式，在这里是指可表示为单项式之和的多重线性形式，其中每个单项式都是系数与试探/测试函数及其导数的乘积。此类可涵盖通过加法，乘法和微分表示的所有形式。早期版本的形式编译器FFC实现了一种简单的形式语言，该语言仅限于这三个操作。现在，这种简单的形式语言已被新的更具表示力的UFL形式语言所取代。结果，张量表示只能应用到可以用UFL表示的形式的子集。这是由FFC自动检查的；如果张量表示不适用，则使用数值正交。

表示定理后来扩展到Rognes等人（2009）的Piola-映射单元，以及Ølgaard等人（2008年）证明了如何为不连续的Galerkin方法计算张量表示。

表8.1 与质量矩阵相关的双线性形式的胞元张量

\(A_T\)

的张量表示

\(A_T = A^0 : G_T\)

。

表8.2 与平流

w \cdot \nabla u

8·3 扩展和限制

张量缩并（8.7）假设来自参考胞元的映射 $$F_T$$ 是仿射的，从而允许将变换 $\partial \hat{x}/\partial x$ 和行列式 $\mathrm{det} \ F'_K$ 从积分中提出来。如果映射是非仿射的（有时称为“高次”映射），则可以对相应有限元空间的基函数进行展开，并将系数从积分中提出，如表8.2中的平流项所示。或者，如Kirby和Logg（2006）所述，可以通过正交来计算胞元张量，并将正交点的和表示为张量缩并。如上所述，张量缩并很容易扩展到由Piola变换所映射的基函数。

这种方法的局限性在于，它要求在胞元 $$T$$ 上的每个基函数，都在仿射的Piola变换下，成为单个参考单元基函数的像。尽管这涵盖了广泛的常用单元，但不包括某些具有基于导数自由度的单元，例如Hermite和Argyris单元。令 $$F_T$$ 是参考单元函数空间到胞元 $$T$$ 上函数空间的映射，例如仿射映射或Piola变换。然后，物理单元基函数可以表示为参考单元基函数变换后的线性组合：

\phi_i^T = \sum^n_{j=1} M_{T,ij} \mathcal{F}_T(\hat{\phi}_j) \tag{8.8}

该矩阵 $$M_T$$ 的结构取决于自由度的种类，并且根据胞元的几何，每个胞元 $$T$$ 的值通常是不同的。通常，矩阵 $$M_T$$ 是稀疏的。给定 $$M_T$$ ，张量缩并框架可被扩展来处理更一般的单元。如前所述，可以通过参考单元基函数映射来计算参考张量 $$A^0$$ 。但是，张量缩并 $$A^0 : G_T$$ 必须通过矩阵 $$M_T$$ 对其进行校正。目前尚未在形式编译器FFC中实现，因此FEniCS不支持Hermite和Argyris单元。

对于许多简单的变分形式，例如上面讨论的泊松方程，质量矩阵和平流项，张量缩并（8.7）导致在数值正交上显着提速，有时甚至高达几个数量级。但是，随着形式的复杂性增加，正交的相对效率也增加。简而言之，形式的复杂性可以通过形式中出现的导数和系数的数量来度量。对于每个导数和系数，参考张量A0的秩增加1。因此，对于泊松方程，由于形式具有两个导数，因此秩为2 + 2 = 4；对于质量矩阵，由于既没有导数也没有系数，秩为2 + 0。对于平流项，秩为2 + 2 + 1 = 5，因为该形式具有一个导数，一个系数和一个内积 $w\cdot\nabla$ 。由于参考张量 $$A^0$$ 的大小随其秩呈指数增长，因此对于高复杂度的形式，张量缩并可能会变得非常昂贵。在这些情况下，正交更为有效。正交有时也可能是唯一可用的选择，因为张量缩并不能直接应用于不能表示为系数，试探/测试函数及其导数乘积的简单形式。因此，能够在两种方法之间进行选择非常重要。张量表示有时可能是最有效的方法，而在其他情况下，正交更为有效，甚至是唯一可能的选择。这种权衡有在第7章和第12章中讨论。

【章节目录】