有限元变分形式的正交表示(二)【翻译】
【章节目录】
7·3 性能比较
在本节中,我们研究上一节概述的优化策略对运行时性能的影响。 关键不是要对优化进行严格的分析,而是要提供有关不同策略何时最有效的指示。 我们还将比较正交表示和张量表示的运行时性能(在第8章中进行了介绍),以说明两种方法的优缺点。
7·3·1 正交优化的性能
将使用两种形式来研究正交优化的性能,即加权拉普拉斯方程(7.1)的双线性形式和第17章方程(17.6)中提供的超弹性模型的双线性形式。 在两种情况下,都将使用二次拉格朗日有限元。
所有测试均在1.7GHz的Intel Pentium M CPU上进行,带有1.0GB的RAM,运行带有Linux内核2.6.38的Ubuntu 11.10。 我们使用Python v2.7.2和NumPy v1.5.1(均与FFC有关)和g++ v4.6.1来编译符合UFC v2.0.2的C++代码。
用不同的FFC优化来编译这两种形式,并确定用于计算局部单元张量的浮点运算(flops)次数。 我们将浮点运算(flops)次数定义为代码中“ +”和“ *”运算符所有出现的次数总和。 还可以计算当前FFC优化与标准正交表示的浮点运算次数比(“o/q”)。 然后使用四个不同的优化选项,通过g++编译生成代码,并测量计算单元张量N次所需的时间。 在下面的代码中,我们将用-zeros作为-f eliminate_zeros选项的简写,用-simplify作为-f simplify_expressions选项的简写,用-ip作为-f precompute_ip_const选项的简写,用-basis作为-f precompute_basis_const选项的简写 。
表7.1显示了具有不同FFC优化的加权拉普拉斯方程的运算次数,而图7.6显示了 \(N = 1 \times 10^7\) 时不同编译器选项的运行时性能。 FFC编译器选项可以在图的x轴上看到,并且四个g++编译器选项以不同的颜色显示。
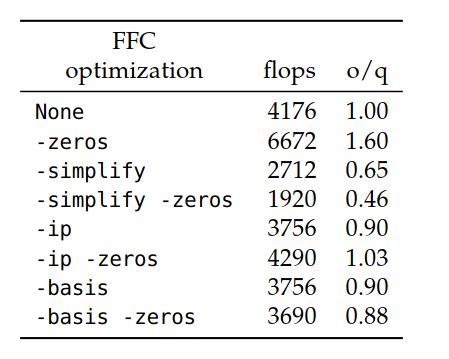
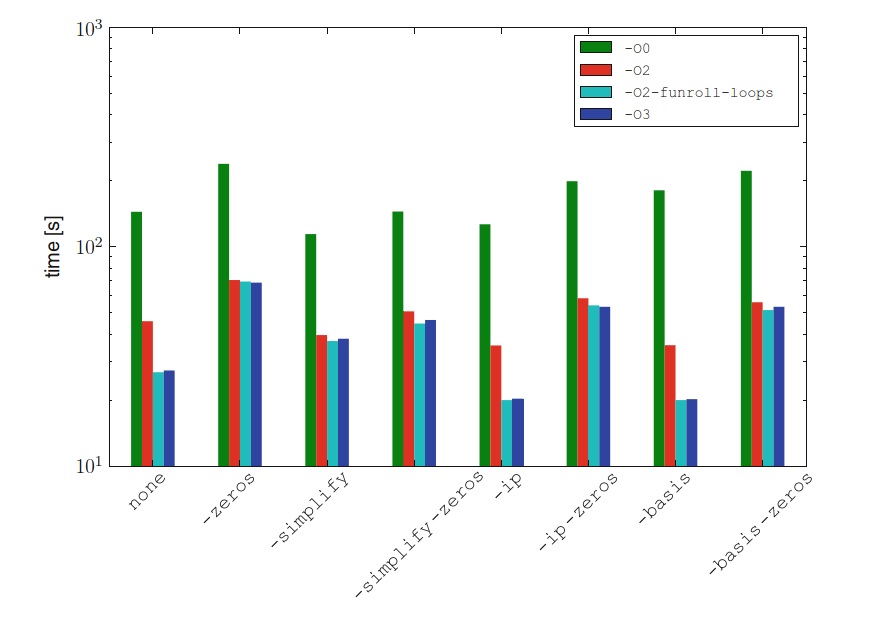
对所有的优化选项,FFC和g++编译时间均不到2秒。 从图7.6可以明显看出,g++优化极大地影响了运行时性能。 与不使用g++优化(-O0标记)的情况相比,使用-O2选项时,标准正交代码的运行时间改善了3.31倍,使用-O2 -funroll-loops选项时,改善了5.23倍, -O3选项时为7.75。 使用FFC优化选项-zeros时,-O3选项似乎不会明显改善-O2 -funroll-loops选项的运行时间。 单独使用FFC优化选项-zeros不能改善运行时性能。 实际上,即使将此选项与-simplify选项组合使用,使用此选项与任何其他优化选项的组合也会增加运行时间,与标准的正交表示相比,该选项的操作数明显减少。 值得注意的一点是,如果没有g++优化,即使-ip和-basis选项在运行时存在相同的浮点运算次数,它们在运行时也存在很大差异。 启用g++优化后,将完全消除这种差异,并且两个FFC优化的运行时间相同。 这表明不可能仅凭操作次数就可以预测运行时性能,因为必须考虑FFC优化的类型以及g++编译器选项的预期用途。 这种形式的优化的最佳组合是FFC选项-ip或-basis与g++选项-O3组合,在这种情况下,与没有g++优化的标准正交代码相比,运行时间改善了10.2倍。
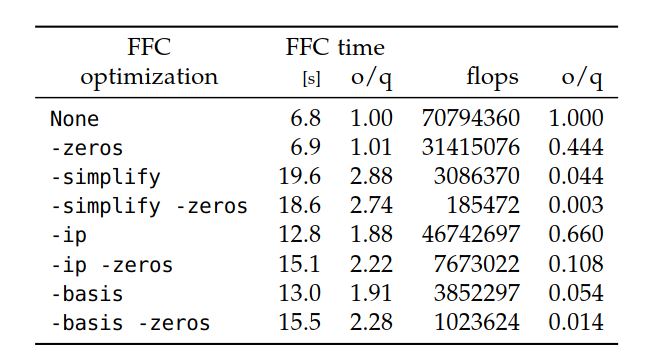
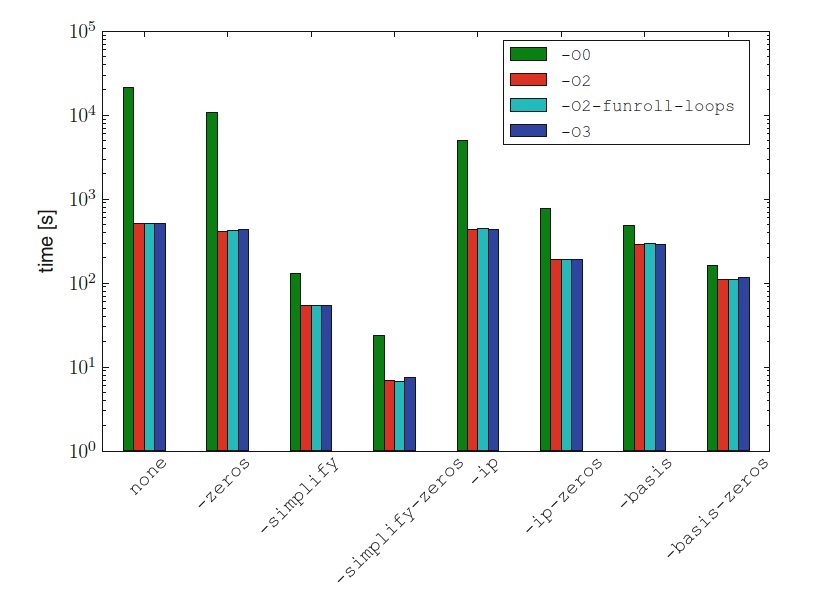
表7.2给出了具有不同FFC优化的超弹性的双线性形式的操作次数和FFC编译时间,而图7.7显示了
\(N = 1 \times 10^4\)
时不同编译器选项的运行时性能。 计算单元张量所涉及的浮点运算次数,与加权拉普拉斯示例进行比较,很明显,这个问题要复杂得多。 表7.2中的FFC编译时间表明,-simplify优化,正如预期,是执行成本最高的。 对于所有优化选项,所有测试用例的g++编译时间在2到7秒之间。 需要注意的一点是,该问题减少浮点运算次数的范围比加权拉普拉斯问题大得多,不同FFC优化之间的浮点运算次数差异跨越几个数量级。 相比之下,加权拉普拉斯问题的未经优化和最有效的优化策略之间的差异大约为2倍。 在不使用g++优化的情况下,超弹性问题的运行时性能可以直接与浮点运算的次量相关。 当g++优化-O2打开时,此效果变得不太明显。 与g++优化有关的另一点要注意的是,启用-O2以外的其他优化似乎并不能在运行时提供任何进一步的改进。 对于超弹性示例,选项-zeros会对性能产生积极影响,不仅是单独使用时,尤其是与其他FFC优化结合使用时。 这与加权拉普拉斯方程相反。 原因是测试和试探函数是矢量值而不是标量值,从而可以消除更多的零。 最后,请注意,与加权拉普拉斯问题相比,-simplify选项在此示例中的效果特别好。 原因是超弹性形式的性质会导致要用相对复杂的表达式来计算局部单元张量中的项。 但是,此表达式仅包含几个不同的变量(雅可比的逆分量和基函数),这使-simplify选项非常有效,因为许多项是通用的并且可以预先计算和外提的。 对于超弹性形式,优化的最佳组合是FFC选项-simplify -zeros和g++选项-O2 -funroll-loops,与使用FFC或g++而没有优化的情况相比,该代码将代码的运行时性能提高了335倍 。
对于所考虑的示例,很明显,没有一种优化策略可以在所有情况下都达到最佳。 此外,生成阶段优化能作到最好的程度,取决于g++编译器执行的优化。 对于上述测试案例,不同的C++编译器也很有可能给出不同的结果。 因此,为选择适当的生产代码优化,一般的建议是,选择应基于针对特定问题的基准程序。
7·3·2 正交和张量表示的相对性能
如上一节所述,给定类型的优化可能对一类形式有效,而对另一类形式则无效。 类似地,对于不同的方程,可以在正交和张量表示之间观察到差异。 Ølgaard和Wells(2010)对此问题进行了详细研究。 为方便起见,我们在此用表7.3重现这篇论文的主要结论。 本节中显示的结果与二维的类弹性双线性形式有关,该形式预先乘以了多个标量系数 \(f_i\) :
\[ a(u,v)=\int_\Omega{(f_0 f_1,\dots,f_{n_f})\nabla^su : \nabla^s v dx} \tag{7.7} \]其中, \(n_f\) 是预乘系数的个数。 测试和试探函数用 \(v, u \in V_h\) 表示,其中
\[ V_h = \left\{v \in [H^1(\Omega)]^2 : v|_T \in [P_q(T)]^2 \ \forall T \in \mathcal{T}\right\} \tag{7.8} \]和系数函数 \(f_i \in W_h\) ,其中
\[ W_h = \left\{f \in H^1(\Omega) : f|_T \in P_p(T) \ \forall T \in \mathcal{T} \right\}\tag{7.9} \]其中
\(q\)
和
\(p\)
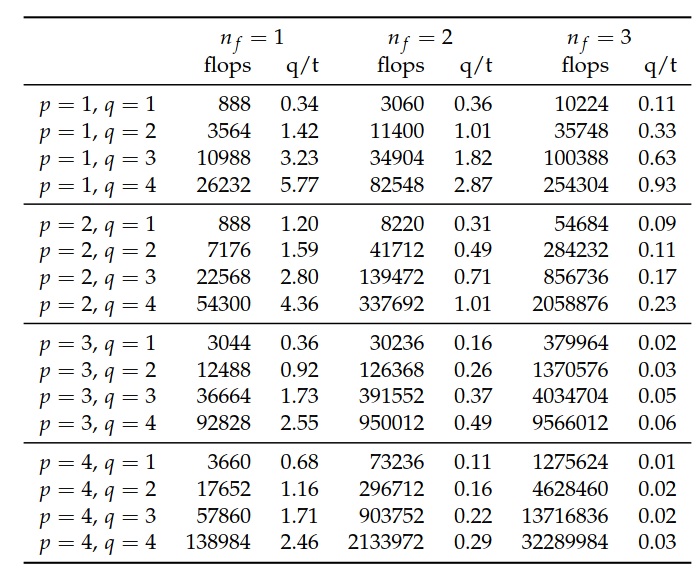
表示拉格朗日基函数的多项式次数。 系数的个数和多项式的次数是变化的,并且同时记录用张量和正交表示计算局部单元张量所需的浮点运算次数。 通过对正交表示使用优化选项-f eliminate_zeros -f simplify_expressions可获得结果。 在表7.3中,给出了正交表示和张量表示的浮点运算次数比(q/t)。 对浮点运算次数,比率q/t>1表示张量表示更有效,而q/t<1表示正交表示更有效。 在比较两个表示形式的运行时性能时,浮点运算次数是性能的良好指标。 但是,正如我们在上一节中所显示的,对于给定的形式,具有最低浮点运算次数的正交代码并不总是表现最佳。 此外,运行时性能甚至取决于所使用的g++选项。 这就产生了一个问题,即是否有可能仅根据浮点运算次数的估计在表示之间进行良好的选择,如Ølgaard和Wells(2010)所建议的那样。
但是,仍然可以从表中读取一些一般趋势。 形式中增加系数函数的个数 \(n_f\) ,显然有利于正交表示。 对于 \(n_f=3\) ,可以期望正交表示对于 \(q\) 和 \(p\) 的所有值表现最佳。 增加系数的多项式次数 \(p\) 也有助于正交表示,尽管与增加系数的效果相比,效果不那么明显。 当测试和试探函数的多项式次数 \(q\) 增加时,张量表示似乎表现更好,尽管当系数变低时效果最明显。
7·4 表示的自动选择
我们已经说明了如何通过为FFC和g++编译器使用各种优化选项,以及通过更改形式的表示来改善变分形式生成代码的运行时性能。 选择形式表示和优化选项的组合以实现最佳性能将不可避免地需要一个所研究特定问题的基准。 但是,通常需要许多复杂程度不同的变分形式来解决更复杂的问题。 为所有这些设置基准既麻烦又耗时。 此外,在模型开发阶段,与变分形式的快速原型制作相比,运行时性能至关重要,只要生成的代码执行得相当好即可。
因此,FFC的默认是用张量表示的成本测量来自动确定应使用哪种形式表示。 简而言之,成本简单地计算为代表形式的单项式中存在的系数和导数个数之和的最大值。 如果此成本大于当前设置为3的指定阈值,则选择正交表示。 回顾表7.3,当 \(n_f=3\) 时,对于几乎所有测试用例,正交表示的浮点运算次数显着降低。 尽管这种方法似乎是临时的,但对于运行时性能差异非常明显的情况,它会很好地起作用。 重要的是要记住,生成的代码仅与局部单元张量的求值有关,并且值插入稀疏矩阵和求解方程组所需的时间将会降低任何差异,尤其是对于简单形式。 因此,对于运行时性能差异较小的形式,正确选择表示的重要性不那么重要。 未来的改进可能是设计一种策略,使系统也可以自动为正交表示选择优化策略。
【章节目录】