常见有限元(二)【翻译】
【章节目录】
3·4 H(div)有限元
Sobolev空间
\(H(\mathrm{div})\)
由分量和弱散度(the weak divergence)都平方可积的矢量场组成。 这是一个比d-矢量场(
\([H^1]^d, \quad d \ge 2\)
)还要更弱的要求。 这个空间自然是与二阶椭圆问题,多孔介质流和弹性方程的混合形式有关的。 对于
\(H(\mathrm{div})\)
-符合的有限元族,虽然每个分量不必是连续的,但是法向分量必须是连续的。 为了确保这种连续性,
\(H(\mathrm{div})\)
-符合的单元的自由度通常包括单元的维面(facets)上的法向分量。
\(H(\mathrm{div})\)
-符合的两个主要单元族是Raviart–Thomas单元和Brezzi–Douglas–Marini单元。这两个族如后所述。 此外还包括:可以离散化具有平方可积的逐行散度对称张量场空间的Arnold-Winther单元,和Mardal-Tai-Winther单元。 【译者注:所谓逐行散度(row-wise divergence),比如对矩阵而言,就是对每行求散度】
3·4·1 Raviart–Thomas单元
Raviart-Thomas单元由Raviart和Thomas(1977)引入。 这是对三角形上二阶椭圆方程混合形式离散化的第一个单元。 这个单元的空间 \(\mathcal{V}\) 被设计成最小多项式空间 \(\mathcal{V} \subset \mathcal{P}_q(T), \quad q = 1, 2, \dots\) ,从中可以将散度映射到 \(\mathcal{P}_{q-1}(T)\) 。 此后不久,Nédélec(1980)将其扩展到四面体和方盒体。 因此,有时也将其称为Raviart–Thomas–Nédélec单元。 在这里,我们将其二维和三维的版本都标记为Raviart–Thomas单元。
以下给出的定义是基于Nédélec(1980)(和Brezzi和Fortin(1991))提出的。 原始的Raviart–Thomas论文使用略有不同的形式。 此外,Raviart和Thomas最初是从 \(q=0\) 开始计数的。 因此,这种最低阶次的单元,传统上被称为 \(\mathrm{RT}_0\) 单元。 为了保持一致性,这种 \(\mathcal{P}_q(T)\) 中的多项式有限元阶次 \(q\) ,我们在这里改用 \(q=1\) 来标记最低阶次单元(Nédélec也是如此) 。
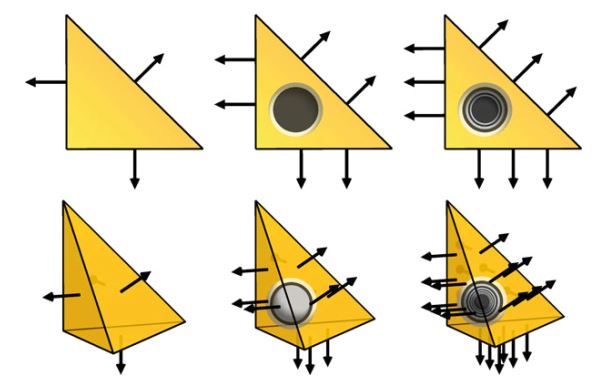
定义3.5(Raviart–Thomas单元) Raviart–Thomas单元( \(\mathrm{RT}_q, \quad q = 1, 2, \dots\) )的定义为:
\[ T \in \{\mathrm{triangle}, \mathrm{tetrahedron}\} \tag{3.18} \] \[ \mathcal{V} = [\mathcal{P}_{q-1}(T)]^d + x \mathcal{P}_{q-1}(T) \tag{3.19} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_f{ v \cdot n p ds} & \quad \text{ 对基函数集 } p \in \mathcal{P}_{q-1}(f) \ \text{ 对每个维面 } f \\ \int_T v \cdot p dx & \quad \text{ 对基函数集 } p \in [\mathcal{P}_{q-2}(T)]^d, \ q \ge 2 \end{aligned}\right. \tag{3.20} \]例如,三角形上最低阶次Raviart–Thomas空间是一个三维空间,由以下形式的矢量场组成
\[ v(x) = \alpha + \beta x \tag{3.21} \]其中, \(\alpha\) 是矢量值常量, \(\beta\) 是标量常量。
\(\mathrm{RT}_q\) 的维数:
\[ n(q) = \left\{\begin{aligned}q(q+2) & \quad T \ \mathrm{triangle} \\ \frac{1}{2}q(q+1)(q+3) & \quad T \ \mathrm{tetrahedron} \end{aligned}\right. \tag{3.22} \]令 \(\Pi^q_T, q = 1, 2, \dots\) 表示由自由度定义的插值算符,我们有(Brezzi和Fortin,1991,第III.3章)。
\[ \begin{aligned}\|u - \Pi^q_T u\|_{H(\mathrm{div})(T)} &\le C h^q_T|u|_{H^{q+1}(T)} \\ \|u - \Pi^q_T u\|_{L^2(T)} &\le C h^q_T|u|_{H^q(T)} \end{aligned} \tag{3.23} \]3·4·2 Brezzi–Douglas–Marini单元
Brezzi–Douglas–Marini单元由Brezzi,Douglas和Marini在Brezzi等人(1985a)的二维(三角形)基础上引入的。 这个单元可被看作是使用完全多项式空间的Raviart–Thomas单元的另一种选择。 后来被Nédélec(1986)和Brezzi等人(1987a)将其扩展到三维的(四面体,棱柱和立方体)。 此处给出的定义基于Nédélec(1986)的。
引入Brezzi–Douglas–Marini单元,可用于二阶椭圆方程的混合公式。 但是,它对于弹性应力张量的弱对称离散化也是有用的。 参见Farhloul和Fortin(1997); Arnold等(2007) 。
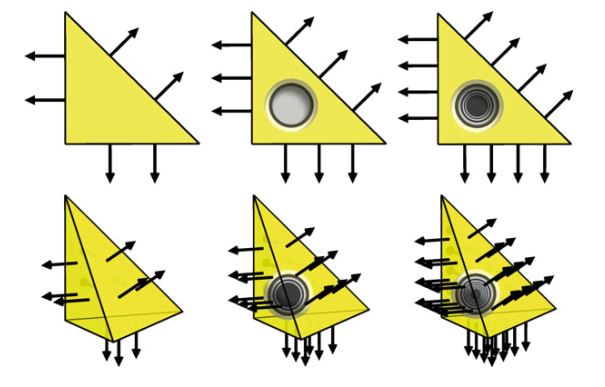
定义3.6(Brezzi–Douglas–Marini单元) Brezzi–Douglas–Marini单元( \(\mathrm{BDM}_q,\quad q = 1, 2, \dots\) )的定义为
\[ T \in \{\mathrm{triangle}, \mathrm{tetrahedron}\} \tag{3.24} \] \[ \mathcal{V} = [\mathcal{P}_q(T)]^d \tag{3.25} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_f{ v \cdot n p ds} & \quad \text{ 对基函数集 } p \in \mathcal{P}_q(f) \ \text{ 对每个维面 } f \\ \int_T v \cdot p dx & \quad \text{ 对基函数集 } p \in \mathrm{NED}^1_{q-1}(T), \ q \ge 2 \end{aligned}\right. \tag{3.26} \]其中, \(\mathrm{NED}^1\) 指是后面第3.5.1节中定义的第一种Nédélec \(H(\mathrm{curl})\) 单元。
\(\mathrm{BDM}_q\) 的维数:
\[ n(q) = \left\{\begin{aligned}(q+1)(q+2) & \quad T \ \mathrm{triangle} \\ \frac{1}{2}(q+1)(q+2)(q+3) & \quad T \ \mathrm{tetrahedron} \end{aligned}\right. \tag{3.27} \]令 \(\Pi^q_T,\quad q = 1, 2, \dots\) 表示由自由度定义的插值算符,于是有(Brezzi和Fortin,1991,第III.3章):
\[ \begin{aligned}\|u - \Pi^q_T u\|_{H(\mathrm{div})(T)} &\le C h^q_T|u|_{H^{q+1}(T)} \\ \|u - \Pi^q_T u\|_{L^2(T)} &\le C h^{q+1}_T|u|_{H^{q+1}(T)} \end{aligned} \tag{3.28} \]Brezzi–Douglas–Marini单元的一个轻微修改,约束在单元空间 \(\mathcal{V}\) 上,通过仅允许 \(q-1\) 次多项式(而不是 \(q\) 次完全多项式)在边界的法向分量。 Brezzi等人(1987b)在矩形上建议使用这种单元,并且Brezzi和Fortin(1991)也给出了在三角形上的类似的物。 以类似的精神,Brezzi等人(1985b),在合适的边界上,调整三角形间的多项式阶次,推导出具有不同阶次的单元。
3·4·3 Mardal–Tai–Winther单元
Mardal-Tai-Winther单元由Mardal等人 (2002)引入,用作适用于二维Darcy和Stokes流速度空间的有限元。 在Darcy流方程中,速度空间仅要求 \(H(\mathrm{div})\) -正则性。 此外,基于 \(H^1\) -符合的有限元的离散化通常不稳定。 另一方面,对于Stokes方程,速度空间明确规定了 \(H^1\) -正则性。 Mardal–Tai–Winther单元是 \(H(\mathrm{div})\) -符合的,但是 \(H^1\) -不符合的。 在Tai和Winther(2006)中,该单元被扩展到三维,但是在这里我们仅介绍二维情况。
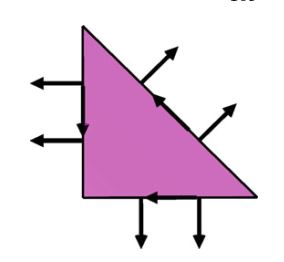
定义3.7(Mardal–Tai–Winther单元) Mardal–Tai–Winther单元 ( \(\mathrm{MTW}\) )被定义为:
\[ T = \mathrm{triangle} \tag{3.29} \] \[ \begin{aligned}\mathcal{V} = \{v &\in [\mathcal{P}_3(T)]^2, \\ & \qquad \mathrm{s.t.} \ \mathrm{div}\ v\in\mathcal{P}_0(T) \text{ and } v\cdot n|_f\in\mathcal{P}_1(T),\\ &\qquad \qquad \text{ 对每个维面}f \} \end{aligned} \tag{3.30} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_f{ v \cdot n p ds} & \quad \text{ 对基函数集 } p \in \mathcal{P}_1(f) \text{ 对每个维面} f \\ \int_f v \cdot t dx & \quad \text{ 对每个维面} f \end{aligned}\right. \tag{3.31} \]\(\mathrm{MTW}\) 的维数为:
\[ n = 9 \tag{3.32} \]令 \(\Pi_T\) 表示由自由度定义的插值算子,我们有
\[ \begin{aligned}\|u - \Pi_T u\|_{H^1(T)} &\le C h_T|u|_{H^2(T)} \\ \|u - \Pi_T u\|_{H(\mathrm{div})(T)} &\le C h_T|u|_{H^2(T)} \\ \|u - \Pi_T u\|_{L^2(T)} &\le C h^2_T|u|_{H^2(T)} \end{aligned} \tag{3.33} \]3·4·4 Arnold–Winther单元
Arnold-Winther单元由Arnold和Winther(2002)引入。 这篇论文提出了用于线性弹性应力-位移公式的首个稳定的混合(非复合)有限元。 被用于应力空间的这种有限元,在这里表示为Arnold-Winther单元。 此有限元是一个逐行 \(H(\mathrm{div})\) -符合的对称张量单元。 此有限元是为多项式阶次的层次结构引入的,并且被Adams和Cockburn(2005)和Arnold等人(2008年)扩展到了三维。 但这里我们仅介绍最低阶次的二维情况。
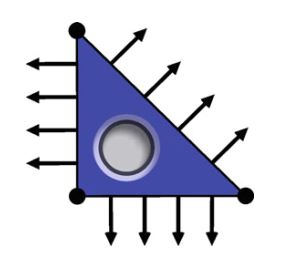
定义3.8(Arnold–Winther单元) (最低阶次)Arnold–Winther单元 ( \(\mathrm{AW}\) )被定义为:
\[ T = \mathrm{triangle} \tag{3.34} \] \[ \mathcal{V} = \left\{v\in\mathcal{P}_3(T;S): \mathrm{div}\ v\in \mathcal{P}_1(T;\mathbb{R}^2) \right\} \tag{3.35} \] \[ \mathcal{L} = \left\{\begin{aligned}v(x^k)_{ij} & \quad 1 \le i \le j \le 2 \ \text{在每个顶点} x^k \\ \int_f{ \sum^2_{j=1}{v_{ij} n_j} p ds} & \quad \text{ 对基函数集 } p \in \mathcal{P}_1(f), \\ & \qquad \text{ 对每个维面} f,\ 1 \le i \le 2 \\ \int_T v_{ij} dx & \quad 1 \le i \le j \le 2 \end{aligned}\right. \tag{3.36} \]\(\mathrm{AW}\) 的维数为:
\[ n = 24 \tag{3.37} \]令 \(\Pi_T\) 表示由自由度定义的插值算子,我们有
\[ \begin{aligned}\|u - \Pi_T u\|_{H(\mathrm{div})(T)} &\le C h^2_T|u|_{H^3(T)} \\ \|u - \Pi_T u\|_{L^2(T)} &\le C h^3_T|u|_{H^3(T)} \end{aligned} \tag{3.38} \]3·5 H(curl)有限元
Sobolev空间 \(H(\mathrm{curl})\) 经常出现在与电磁有关的问题中。 Nédélec单元(俗称边单元)被广泛用于解决此类问题,并且是“非标准”(即非最低拉格朗日)有限元的典范(Nédélec,1980,1986)。 为了使分段多项式成为 \(H(\mathrm{curl})\) -符合的,切向分量必须是连续的。 因此, \(H(\mathrm{curl})\) -符合的有限元的自由度通常包括切向分量。
Nédélec(1980,1986)在论文中引入了四族有限元空间。 第一篇论文(1980年)介绍了四面体,立方体和棱柱上的两个有限元空间族:一个是 \(H(\mathrm{div})\) -符合的族,另一个是 \(H(\mathrm{curl})\) -符合的族。 这两个族分别被称为第一种Nédélec \(H(\mathrm{div})\) 单元和第一种Nédélec \(H(\mathrm{curl})\) 单元。 \(H(\mathrm{div})\) 单元可以看作是Raviart–Thomas单元的三维扩展。(因此,作为前面的Raviart–Thomas单元而呈现。) 后面将介绍第一种Nédélec \(H(\mathrm{curl})\) 单元。
第二篇论文(1986年)介绍了更多的有限元空间族: 相应有, 一个是 \(H(\mathrm{div})\) -符合的族, 另一个是 \(H(\mathrm{curl})\) -符合的族。 相应的,这两个族分别被称为第二种Nédélec \(H(\mathrm{div})\) 单元和第二种Nédélec \(H(\mathrm{curl})\) 单元。 \(H(\mathrm{div})\) 单元可看作是Brezzi–Douglas–Marini单元的三维扩展。 (因此,作为前面的Brezzi–Douglas–Marini单元而呈现。) 后面将介绍第二种Nédélec \(H(\mathrm{curl})\) 单元。
Nédélec在他的两篇经典论文中只考虑了三维情况。 但是,也可以定义一个二维curl和二维
\(H(\mathrm{curl})\)
-符合的有限元空间。 在此,我们在三角形上展示Nédélec单元。 尽管是否能将这些单元归到Nédélec名下不得而知,但出于完整性考虑,我们还是将它们包括在内。
Nédélec的工作在许多方面都预见了Arnold等人(2006a)最近提出的有限元外微积分。 ,其中第一种空间表现为
\(\mathcal{P}_q^-\Lambda^k\)
空间,第二种则表现为
\(\mathcal{P}_q\Lambda^k\)
。 此外,在Nédélec(1980)中使用微分算子(弹性应变)来表征函数空间,预示着Arnold等人(2006b)使用的微分复形(differential complexes)。
3·5·1 第一种Nedelec H(curl)单元
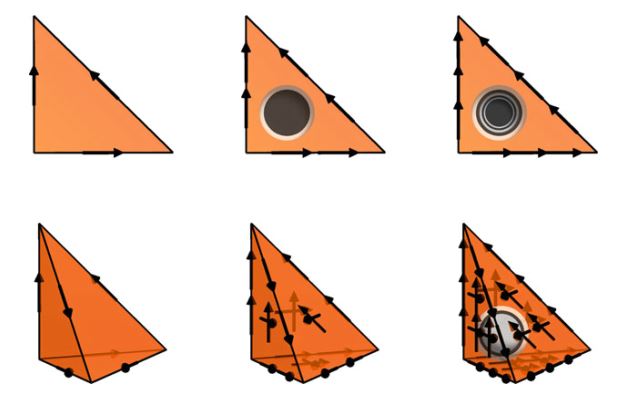
定义3.9(第一种Nédélec H(curl)单元) 对 \(q = 1, 2, \dots\) , 定义空间:
\[ S_q(T) = \left\{s \in [\mathcal{P}_q(T)]^d : s(x) \cdot x = 0 \quad \forall x \in T\right\} \tag{3.39} \]第一种Nédélec单元 ( \(\mathrm{NED}^1_q,\quad q = 1, 2, \dots\) )被定义为(二维的情况):
\[ T = \mathrm{triangle} \tag{3.40} \] \[ \mathcal{V} = [\mathcal{P}_{q-1}(T)]^2 + S_q(T) \tag{3.41} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_e{ v \cdot t p ds} & \quad \text{ 对基函数集 } p \in \mathcal{P}_{q-1}(e) \text{ 对每个边} e \\ \int_T v \cdot p dx & \quad \text{ 对基函数集 } p \in [\mathcal{P}_{q-2}(T)]^2,\quad q \ge 2 \end{aligned}\right. \tag{3.42} \]其中t是边的切线; 对于的三维情况:
\[ T = \mathrm{tetrahedron} \tag{3.43} \] \[ \mathcal{V} = [\mathcal{P}_{q-1}(T)]^3 + S_q(T) \tag{3.44} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_e{ v \cdot t p dl} & \quad \text{ 对基函数集 } p \in \mathcal{P}_{q-1}(e) \text{ 对每个边} e \\ \int_f{ v \times n \cdot p ds} & \quad \text{ 对基函数集 } p \in [\mathcal{P}_{q-2}(f)]^2, \\ &\qquad \qquad \text{ 对每个面} f, \quad q \ge 2 \\ \int_T v \cdot p dx & \quad \text{ 对基函数集 } p \in [\mathcal{P}_{q-3}]^3,\quad q \ge 3 \end{aligned}\right. \tag{3.45} \]\(\mathrm{NED}^1_q\) 的维数为:
\[ n(q) = \left\{\begin{aligned}q(q+2) & \quad T \ \mathrm{triangle} \\ \frac{1}{2}q(q+2)(q+3) & \quad T \ \mathrm{tetrahedron} \end{aligned}\right. \tag{3.46} \]令 \(\Pi^q_T\) 表示由上面的自由度定义的插值算符,我们有(Nédélec, 1980, 定理2)
\[ \begin{aligned}\|u - \Pi^q_T u\|_{H(\mathrm{curl})(T)} &\le C h^q_T|u|_{H^{q+1}(T)} \\ \|u - \Pi^q_T u\|_{L^2(T)} &\le C h^q_T|u|_{H^q(T)} \end{aligned} \tag{3.47} \]3·5·2 第二种Nedelec H(curl)单元
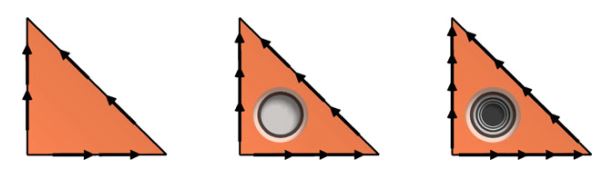
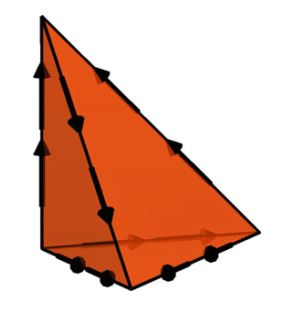
定义3.10(第二种Nédélec H(curl)单元) 第二种Nédélec单元( \(\mathrm{NED}^2_q,\quad q = 1, 2, \dots\) )被定义为(二维的情况):
\[ T = \mathrm{triangle} \tag{3.48} \] \[ \mathcal{V} = [\mathcal{P}_q(T)]^2 \tag{3.49} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_e{ v \cdot t p ds} & \quad \text{ 对基函数集 } p \in \mathcal{P}_q(e) \text{ 对每个边} e \\ \int_T v \cdot p dx & \quad \text{ 对基函数集 } p \in \mathrm{RT}_{q-1}(T),\quad q \ge 2 \end{aligned}\right. \tag{3.50} \]其中t是边的切线; 对于的三维情况:
\[ T = \mathrm{tetrahedron} \tag{3.51} \] \[ \mathcal{V} = [\mathcal{P}_q(T)]^3 \tag{3.52} \] \[ \mathcal{L} = \left\{\begin{aligned}\int_e{ v \cdot t p dl} & \quad \text{ 对基函数集 } p \in \mathcal{P}_q(e) \text{ 对每个边} e \\ \int_f{ v \cdot p ds} & \quad \text{ 对基函数集 } p \in \mathrm{RT}_{q-1}(f), \\ &\qquad \qquad \text{ 对每个面} f, \quad q \ge 2 \\ \int_T v \cdot p dx & \quad \text{ 对基函数集 } p \in \mathrm{RT}_{q-2}(T),\quad q \ge 3 \end{aligned}\right. \tag{3.53} \]\(\mathrm{NED}^2_q\) 的维数为:
\[ n(q) = \left\{\begin{aligned}(q+1)(q+2) & \quad T \ \mathrm{triangle} \\ \frac{1}{2}(q+1)(q+2)(q+3) & \quad T \ \mathrm{tetrahedron} \end{aligned}\right. \tag{3.54} \]令 \(\Pi^q_T\) 表示由上面的自由度定义的插值算符,我们有(Nédélec, 1986, 命题3)
\[ \begin{aligned}\|u - \Pi^q_T u\|_{H(\mathrm{curl})(T)} &\le C h^q_T|u|_{H^{q+1}(T)} \\ \|u - \Pi^q_T u\|_{L^2(T)} &\le C h^{q+1}_T|u|_{H^{q+1}(T)} \end{aligned} \tag{3.55} \]【章节目录】